题目内容
如图，以向量| OA |
| a |
| OB |
| b |
| BM |
| 1 |
| 3 |
| BC |
| CN |
| 1 |
| 3 |
| CD |
| a |
| b |
| OM |
| ON |
| MN |
分析：根据向量加法的平行四边形法则，得
=
+
，从而得到
=
（
+
）．由向量减法法则得
=（
-
），从而得到
=
=
（
-
），进而算出
=
+
=
+
，最后得到
=
-
=
-
．
| OD |
| a |
| b |
| ON |
| 2 |
| 3 |
| a |
| b |
| BA |
| a |
| b |
| BM |
| 1 |
| 3 |
| BC |
| 1 |
| 6 |
| a |
| b |
| OM |
| OB |
| BM |
| 1 |
| 6 |
| a |
| 5 |
| 6 |
| b |
| MN |
| ON |
| OM |
| 1 |
| 2 |
| a |
| 1 |
| 6 |
| b |
解答：解：∵四边形OADB是平行四边形，
∴
=
-
=
+
，
=
=
（
-
）=
（
-
）
可得
=
=
（
-
），
由向量加法法则，得
=
+
=
+
（
-
）=
+
∵
=
，
=
=
，
∴
=
+
=
+
×
=
=
（
+
）
由向量减法法则，得
=
-
=
（
+
）-（
+
）=
-
综上，可得
=
+
，
=
（
+
），
=
-
∴
| OD |
| OA |
| OB |
| a |
| b |
| BC |
| 1 |
| 2 |
| BA |
| 1 |
| 2 |
| OA |
| OB |
| 1 |
| 2 |
| a |
| b |
可得
| BM |
| 1 |
| 3 |
| BC |
| 1 |
| 6 |
| a |
| b |
由向量加法法则，得
| OM |
| OB |
| BM |
| b |
| 1 |
| 6 |
| a |
| b |
| 1 |
| 6 |
| a |
| 5 |
| 6 |
| b |
∵
| CN |
| 1 |
| 3 |
| CD |
| OC |
| CD |
| 1 |
| 2 |
| OD |
∴
| ON |
| OC |
| CN |
| 1 |
| 2 |
| OD |
| 1 |
| 3 |
| 1 |
| 2 |
| OD |
| 2 |
| 3 |
| OD |
| 2 |
| 3 |
| a |
| b |
由向量减法法则，得
| MN |
| ON |
| OM |
| 2 |
| 3 |
| a |
| b |
| 1 |
| 6 |
| a |
| 5 |
| 6 |
| b |
| 1 |
| 2 |
| a |
| 1 |
| 6 |
| b |
综上，可得
| OM |
| 1 |
| 6 |
| a |
| 5 |
| 6 |
| b |
| ON |
| 2 |
| 3 |
| a |
| b |
| MN |
| 1 |
| 2 |
| a |
| 1 |
| 6 |
| b |
点评：本题在平行四边形中求向量的线性表示式，着重考查了平面向量的基本定理、向量的加法和减法法则等知识，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
如图，A、B分别是射线OM，ON上的两点，给出下列向量：
给定两个长度为1的平面向量
如图，在平面直角坐标系中，以原点为圆心，单位长度1为半径的圆上有两点A（cosα，sinα），B（cosβ，sinβ）．（0＜α＜β＜π）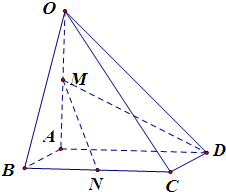
如图，在四棱锥O-ABCD中，底面ABCD是边长为1的正方形，OA⊥底面ABCD，OA=2，M为OA的中点，N为BC中点，以A为原点，建立适当的空间直角坐标系，利用空间向量解答以下问题