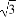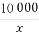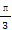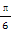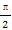Question

设函数f(x)=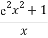,g(x)=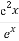,对任意x1,x2∈(0,+∞),不等式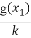≤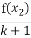恒成立,则正数k的取值范围是　　　　　　.

 

Answer 1

{k|k≥1}

【解析】∵k为正数,∴对任意x1,x2∈(0,+∞),不等式≤恒成立⇒[]max≤[]min

由g'(x)==0,得x=1,

x∈(0,1)时,g'(x)>0,x∈(1,+∞)时,g'(x)<0,

∴[]max==.

同理由f'(x)==0,得x=,

x∈(0,)时,f'(x)<0,x∈(,+∞)时,f'(x)>0,

[]min==,∴≤,k>0k≥1.