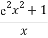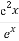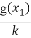Question

已知定义在R上的可导函数f(x)的导函数为f′(x),满足f′(x)<f(x),且f(x+2)为偶函数,f(4)=1,则不等式f(x)<ex的解集为(　　)

(A)(-2,+∞) (B)(0,+∞)

(C)(1,+∞) (D)(4,+∞)

 

Answer 1

B

【解析】因为f(x+2)为偶函数,

所以f(2-x)=f(x+2),因此f(0)=f(4)=1.

令h(x)=,则原不等式即为h(x)<h(0).

又h'(x)==,

依题意f'(x)<f(x),故h'(x)<0,因此函数h(x)在R上是减函数,所以由h(x)<h(0)得x>0.