题目内容
已知定义在R上的函数f(x-1)的对称中心为(1,0),且f(x+2)=-f(x),当x∈(0,1]时,f(x)=2x-1,则f(x)在闭区间[-2014,2014]上的零点个数为 .
考点:函数的周期性,根的存在性及根的个数判断
专题:函数的性质及应用
分析:分析函数的周期性和对称性,进而画出函数在一个周期上的图象,分析一个周期内零点的个数,进而得到f(x)在闭区间[-2014,2014]上的零点个数.
解答:
解:∵f(x+2)=-f(x),
∴f(x+4)=-f(x+2)=f(x),
故函数f(x)是T=4的周期函数,
又∵函数f(x-1)的对称中心为(1,0),
∴函数f(x)的对称中心为(0,0),即函数f(x)为奇函数,
∵当x∈(0,1]时,f(x)=2x-1,
∴在一个周期[-2,2)上的图象如下图所示:

由图可得在一个周期[-2,2)上函数有6个零点,
故每个周期[4k-2,4k+2),k∈Z上函数都有6个零点,
[-2014,2014)上共有[2014-(-2014)]÷4=1007个周期,
故[-2014,2014)共有6×1007=6042个零点,
由f(2014)=0,
故f(x)在闭区间[-2014,2014]上的零点个数为6043,
故答案为:6043
∴f(x+4)=-f(x+2)=f(x),
故函数f(x)是T=4的周期函数,
又∵函数f(x-1)的对称中心为(1,0),
∴函数f(x)的对称中心为(0,0),即函数f(x)为奇函数,
∵当x∈(0,1]时,f(x)=2x-1,
∴在一个周期[-2,2)上的图象如下图所示:

由图可得在一个周期[-2,2)上函数有6个零点,
故每个周期[4k-2,4k+2),k∈Z上函数都有6个零点,
[-2014,2014)上共有[2014-(-2014)]÷4=1007个周期,
故[-2014,2014)共有6×1007=6042个零点,
由f(2014)=0,
故f(x)在闭区间[-2014,2014]上的零点个数为6043,
故答案为:6043
点评:本题考查函数图象的作法,函数的周期性,函数的对称性,函数的零点,熟练作出函数的图象是解决问题的关键,属中档题.

练习册系列答案
相关题目
已知函数f(x)=cosx+
x,x∈[0,π],若f(x)在x0处取得极大值,则f(x0)的值为( )
| 1 |
| 2 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
如图所示的流程图,若输出的结果是9,则判断框中的横线上可以填入的最大整数为( )
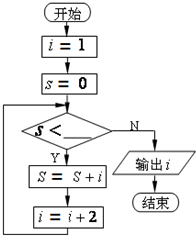

| A、17 | B、16 | C、15 | D、14 |
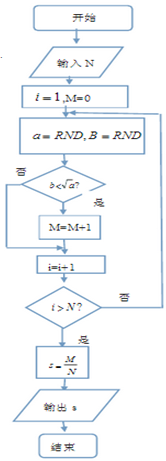 在程序中,x=RND表示将计算机产生的[0,1]区间上的均匀随机数赋给变量x.利用如图的程序框图进行随机模拟,我们发现:随着输入N值的增加,输出的S值稳定在某个常数上.这个常数是
在程序中,x=RND表示将计算机产生的[0,1]区间上的均匀随机数赋给变量x.利用如图的程序框图进行随机模拟,我们发现:随着输入N值的增加,输出的S值稳定在某个常数上.这个常数是