题目内容
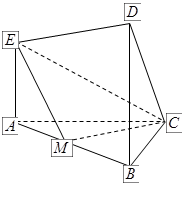
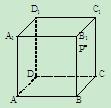
(本题14分)在如图所示的几何体中,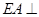 平面
平面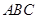 ,
,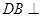 平面
平面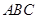
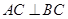 ,且
,且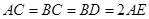 ,
,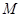 是
是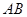 的中点.
的中点.
(I)求证: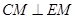 ;
;
(II)求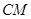 与平面
与平面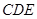 所成的角.
所成的角.
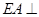 平面
平面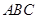 ,
,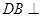 平面
平面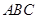
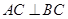 ,且
,且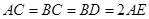 ,
,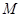 是
是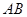 的中点.
的中点.
(I)求证:
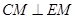 ;
;(II)求
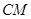 与平面
与平面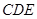 所成的角.
所成的角.(I)证明见解析
(II) .
.
(II)
 .
.方法一:
(I)证明:因为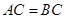 ,
,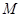 是
是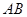 的中点,
的中点,
所以 .
.
又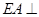 平面
平面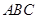 ,
,
所以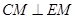 .
.
(II)解:过点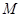 作
作 平面
平面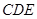 ,垂足是
,垂足是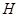 ,连结
,连结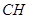 交延长交
交延长交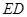 于点
于点 ,连结
,连结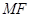 ,
,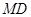 .
.

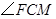 是直线
是直线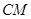 和平面
和平面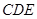 所成的角.
所成的角.
因为 平面
平面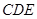 ,
,
所以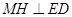 ,
,
又因为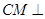 平面
平面 ,
,
所以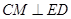 ,
,
则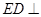 平面
平面 ,因此
,因此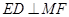 .
.
设 ,
,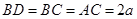 ,
,
在直角梯形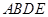 中,
中,
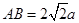 ,
, 是
是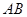 的中点,
的中点,
所以 ,
,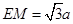 ,
, ,
,
得 是直角三角形,其中
是直角三角形,其中 ,
,
所以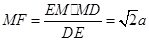 .
.
在 中,
中,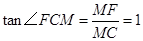 ,
,
所以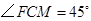 ,
,
故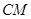 与平面
与平面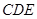 所成的角是
所成的角是 .
.
方法二:
如图,以点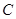 为坐标原点,以
为坐标原点,以 ,
, 分别为
分别为 轴和
轴和 轴,过点
轴,过点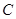 作与平面
作与平面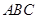 垂直的直线为
垂直的直线为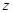 轴,建立直角坐标系
轴,建立直角坐标系 ,设
,设 ,则
,则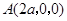 ,
, ,
,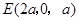 .
. ,
,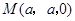 .
.

(I)证明:因为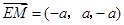 ,
, ,
,
所以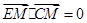 ,
,
故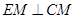 .
.
(II)解:设向量 与平面
与平面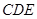 垂直,则
垂直,则 ,
,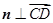 ,
,
即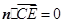 ,
,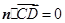 .
.
因为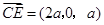 ,
,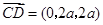 ,
,
所以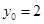 ,
, ,
,
即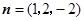 ,
,
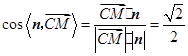 ,
,
直线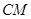 与平面
与平面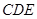 所成的角
所成的角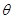 是
是 与
与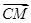 夹角的余角,
夹角的余角,
所以 ,
,
因此直线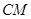 与平面
与平面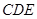 所成的角是
所成的角是 .
.
(I)证明:因为
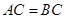 ,
,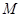 是
是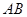 的中点,
的中点,所以
 .
.又
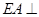 平面
平面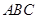 ,
,所以
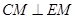 .
.(II)解:过点
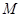 作
作 平面
平面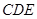 ,垂足是
,垂足是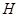 ,连结
,连结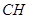 交延长交
交延长交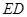 于点
于点 ,连结
,连结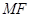 ,
,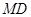 .
.
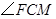 是直线
是直线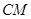 和平面
和平面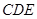 所成的角.
所成的角.因为
 平面
平面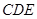 ,
,所以
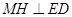 ,
,又因为
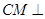 平面
平面 ,
,所以
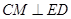 ,
,则
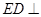 平面
平面 ,因此
,因此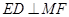 .
.设
 ,
,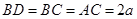 ,
,在直角梯形
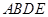 中,
中,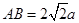 ,
,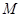 是
是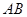 的中点,
的中点,所以
 ,
,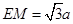 ,
, ,
,得
 是直角三角形,其中
是直角三角形,其中 ,
,所以
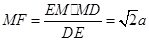 .
.在
 中,
中,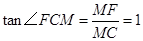 ,
,所以
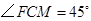 ,
,故
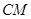 与平面
与平面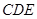 所成的角是
所成的角是 .
.方法二:
如图,以点
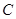 为坐标原点,以
为坐标原点,以 ,
, 分别为
分别为 轴和
轴和 轴,过点
轴,过点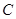 作与平面
作与平面 垂直的直线为
垂直的直线为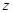 轴,建立直角坐标系
轴,建立直角坐标系 ,设
,设 ,则
,则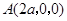 ,
, ,
,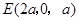 .
. ,
,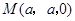 .
.
(I)证明:因为
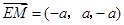 ,
, ,
,所以
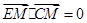 ,
,故
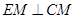 .
.(II)解:设向量
 与平面
与平面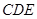 垂直,则
垂直,则 ,
,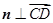 ,
,即
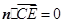 ,
,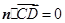 .
.因为
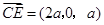 ,
,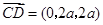 ,
,所以
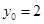 ,
, ,
,即
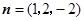 ,
,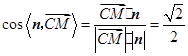 ,
,直线
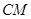 与平面
与平面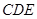 所成的角
所成的角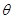 是
是 与
与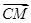 夹角的余角,
夹角的余角,所以
 ,
,因此直线
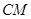 与平面
与平面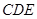 所成的角是
所成的角是 .
.
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
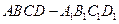 中,
中, 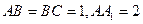 ,
, 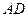 ∥面
∥面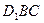 ;
;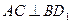 ;
;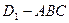 内的概率.
内的概率.
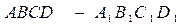 中,求:
中,求: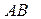 与
与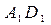 所成的角;
所成的角;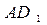 与
与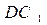 所成的角。
所成的角。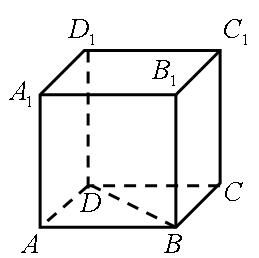
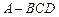 中,
中,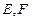 分别是
分别是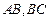 的中点,
的中点,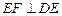 且
且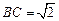 ,若此正三棱锥的四个顶点都在球O的面上,则球O的体积是( )
,若此正三棱锥的四个顶点都在球O的面上,则球O的体积是( )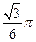
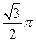
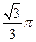
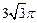
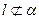 ,则
,则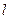 不可能与
不可能与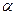 内无数条直线相交。
内无数条直线相交。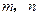 是两条不同的直线,
是两条不同的直线,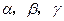 是三个不同的平面,则下列命题中的真命题是( )
是三个不同的平面,则下列命题中的真命题是( )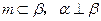 ,则
,则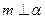
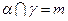
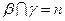 ,
,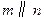 ,则
,则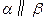
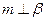 ,
,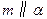 ,则
,则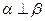
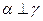 ,
,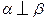 ,则
,则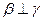
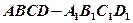 的侧面
的侧面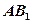 内 有一点
内 有一点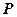 ,它到直线
,它到直线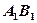 与到直线
与到直线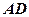 的距离相等,则动点
的距离相等,则动点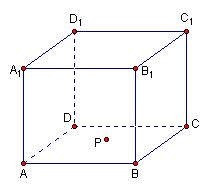
 中,
中, ,
, ,
, ,
, 是棱
是棱 上一动点,
上一动点, 的最小值为
的最小值为