题目内容
已知定义域为 的函数
的函数 是奇函数.
是奇函数.
(1)求 的值;
的值;
(2)用定义法证明函数 在
在 上是减函数;
上是减函数;
(3)若对任意的 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(1) ;(2)详见解析;(3)
;(2)详见解析;(3) .
.
解析试题分析:(1)利用f(0)=0即可解出;(2)利用减函数的定义即可证明;(3)利用函数的奇偶性、单调性即可解出.
试题解析:(1)由 可得
可得
(2)由(1)可得: .
. ,则
,则 ,
,
∴ ,
,
∴ .
.
∴函数f(x)在R上是减函数.
(3)可得 ,
, 函数
函数 为
为 上的减函数
上的减函数
所以有

所以  解得
解得
考点:1.函数奇偶性的性质;2.函数单调性的判断与证明.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知 为虚数单位,且
为虚数单位,且 ,则
,则 的值为( )。
的值为( )。
| A.4 | B. | C. | D. |
 的展开式中各项系数之和为
的展开式中各项系数之和为 ,各项二项式系数之和为
,各项二项式系数之和为 ,且
,且 ,则展开式中含
,则展开式中含 项的系数为 .
项的系数为 . 等于( )
等于( ) ,
, .
. ,命题“
,命题“ 或
或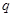 ”为真,求实数
”为真,求实数 的取值范围;
的取值范围; 的取值范围.
的取值范围. 在区间
在区间 上的最大值是2,求实数
上的最大值是2,求实数 的值.
的值. .
. ,求bsinB+csinC的最小值.
,求bsinB+csinC的最小值. ,动点
,动点 与
与 分别在射线
分别在射线 上,且线段
上,且线段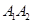 的长为1,线段
的长为1,线段 分别是线段
分别是线段 的中点.
的中点.
 与
与 表示向量
表示向量 ;
; 的交点且平行于直线
的交点且平行于直线 的直线方程
的直线方程