题目内容
13.过点(2,-1)的直线中,被圆x2+y2-2x+4y=0截得的弦长最短的直线方程是( )| A. | x+y-1=0 | B. | x+y+1=0 | C. | x-y+3=0 | D. | x-y-3=0 |
分析 化圆的一般方程为标准方程,求出圆心坐标和半径,画出图形,数形结合求解.
解答  解:化圆x2+y2-2x+4y=0为(x-1)2+(y+2)2=5.
解:化圆x2+y2-2x+4y=0为(x-1)2+(y+2)2=5.
圆心坐标为C(1,-2),半径为$\sqrt{5}$.
∵定点A(2,-1)在圆内,如图:
又${k}_{AC}=\frac{-2-(-1)}{1-2}=1$,
∴过A且与AC垂直的直线的斜率为-1,
∴被圆x2+y2-2x+4y=0截得的弦长最短的直线方程为y+1=-1×(x-2),
即x+y-1=0.
故选:A.
点评 本题考查直线与圆位置关系的应用,考查数形结合的解题思想方法,是中档题.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
2.如图,已知$\overrightarrow{AB}$=a,$\overrightarrow{AC}$=b,$\overrightarrow{BD}$=3 $\overrightarrow{DC}$,用$\vec a$,$\vec b$表示$\overrightarrow{AD}$,则$\overrightarrow{AD}$=( )


| A. | $\vec a$+$\frac{3}{4}$$\vec b$ | B. | $\frac{1}{4}$ $\vec a$+$\frac{3}{4}$$\vec b$ | C. | $\frac{1}{4}$ $\vec a$+$\frac{1}{4}$$\vec b$ | D. | $\frac{3}{4}$ $\vec a$+$\frac{1}{4}$$\vec b$ |
3. n个连续自然数按规律排成表:
n个连续自然数按规律排成表:
根据规律,从2016到2018,箭头的方向依次为( )
 n个连续自然数按规律排成表:
n个连续自然数按规律排成表:根据规律,从2016到2018,箭头的方向依次为( )
| A. | ↓→ | B. | →↑ | C. | ↑→ | D. | →↓ |
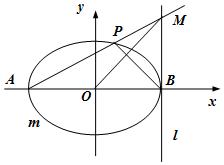 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,且过点$E({1,\frac{3}{2}})$.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,且过点$E({1,\frac{3}{2}})$.