题目内容
7.定义在(-1,0)∪(0,1)的偶函数f(x),满足f($\frac{1}{2}$)=0.当x>0时,总有($\frac{1}{x}$-x)f′(x)•ln(1-x2)>2f(x),则f(x)<0解集为$\{x丨-1<x<-\frac{1}{2}或\frac{1}{2}<x<1\}$.分析 根据偶函数的对称性,利用导函数的性质求函数的单调性,
解答 解:当x>0时,总有($\frac{1}{x}$-x)f′(x)•ln(1-x2)>2f(x)
f′(x)•ln(1-x2)>$\frac{2x}{1-{x}^{2}}f(x)$,
也就是$f′(x)•ln(1-{x}^{2})+\frac{-2x}{1-{x}^{2}}f(x)>0$恒成立,
[ln(1-x2)]′
=[ln(1-x)+ln(1+x)]′
=$\frac{-1}{1-x}+\frac{1}{1+x}$
=$\frac{-2x}{1-{x}^{2}}$
∴[f(x)•ln(1-x2)]′>0恒成立,
设g(x)=f(x)•ln(1-x2),
则g(x)在(0,1)上单调递增
y=ln(1-x2)是偶函数,函数g(x)=f(x)•ln(1-x2)是偶函数,
∴在(-1,0)上单调递减.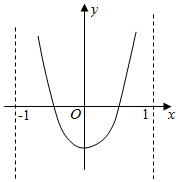
$f(\frac{1}{2})=f(-\frac{1}{2})=0$,$g(\frac{1}{2})=g(-\frac{1}{2})=g(0)=0$
所以g(x)的图象如下:
$x∈(\frac{1}{2},1)$,g(x)>0,而ln(1-x2)<0,所以f(x)<0;
$x∈(0,\frac{1}{2})$,g(x)<0,而ln(1-x2)<0,所以f(x)>0,
函数f(x)的图象对称性可求得解集;
故答案为:$\{x丨-1<x<-\frac{1}{2}或\frac{1}{2}<x<1\}$
点评 本题考查利用函数的对称性及导函数的性质求函数单调区间,属于中档题.

练习册系列答案
相关题目
15.若f(x)=sin(ωx+φ)+cos(ωx+φ)(ω>0)的最小正周期为π,f(0)=$\sqrt{2}$,则( )
| A. | f(x)在$(-\frac{π}{4},\frac{π}{4})$单调递增 | B. | f(x)在$(-\frac{π}{4},\frac{π}{4})$单调递减 | ||
| C. | f(x)在$(0,\frac{π}{2})$单调递增 | D. | f(x)在$(0,\frac{π}{2})$单调递减 |
2.实数x,y满足$\left\{\begin{array}{l}2x+y≤10\\ x+2y≤14\\ x+y≥6\end{array}\right.$,则|x|+|y|的最大值为( )
| A. | 6 | B. | 8 | C. | 10 | D. | 14 |
16.已知sin(α+$\frac{π}{6}$)+cosα=$\frac{4}{5}$$\sqrt{3}$,则cos(2α+$\frac{2π}{3}$)的值为( )
| A. | -$\frac{7}{25}$ | B. | $\frac{7}{25}$ | C. | $\frac{9}{25}$ | D. | -$\frac{9}{25}$ |
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴长为2$\sqrt{3}$,且离心率e=$\frac{1}{2}$,设F1,F2是椭圆的左、右焦点,过F2的直线与椭圆右侧(如图)相交于M,N两点,直线F1M,F1N分别与直线x=4相交于P,Q两点.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴长为2$\sqrt{3}$,且离心率e=$\frac{1}{2}$,设F1,F2是椭圆的左、右焦点,过F2的直线与椭圆右侧(如图)相交于M,N两点,直线F1M,F1N分别与直线x=4相交于P,Q两点.