Question

11．定义min{a，b}=$\left\{\begin{array}{l}{a，a≤b}\\{b，a＞b}\end{array}$，若关于x的方程min$\left\{{2\sqrt{x}，|{x-2}|}\right\}$=m（m∈R）恰有二个不同的实根，则m的值为$2（{\sqrt{3}-1}）$或0．

Answer 1

分析 由2$\sqrt{x}$=|x-2|得x=4+2$\sqrt{3}$或x=4-2$\sqrt{3}$；从而作函数y=min$\left\{{2\sqrt{x}，|{x-2}|}\right\}$的图象，从而解得．

解答 解：令2$\sqrt{x}$=|x-2|，解得，
x=4+2$\sqrt{3}$或x=4-2$\sqrt{3}$；
作函数y=min$\left\{{2\sqrt{x}，|{x-2}|}\right\}$的图象如下，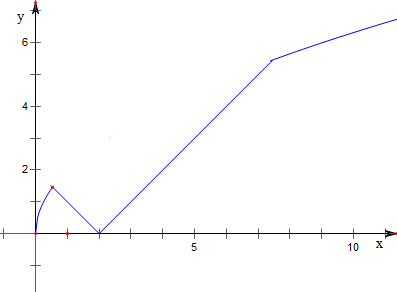

由题意得，当m=0或m=|4-2$\sqrt{3}$-2|=$2（{\sqrt{3}-1}）$时，
方程min$\left\{{2\sqrt{x}，|{x-2}|}\right\}$=m（m∈R）恰有二个不同的实根，
故答案为：$2（{\sqrt{3}-1}）$或0．

点评 本题考查了函数的图象的作法及函数的零点与方程的根的关系应用．