题目内容
6.函数f(x)是R上的奇函数,且当x>0时,函数的解析式为f(x)=$\frac{2}{x}$-1.(1)用定义证明f(x)在(0,+∞)上是减函数;
(2)求当x<0时,函数的解析式.
(3)用分段函数形式写出函数f(x)在R上的解析式.当f(a)=3时,求a的值.
分析 (1)在(0,+∞)上任取x1.x2,且0<x1<x2,利用作差法,可判断函数的单调性;
(2)设x<0,则-x>0,结合函数的奇偶性,可得当x<0时,函数的解析式.
(3)根据(2)中结论,可得函数的解析式,分类讨论满足条件f(a)=3的a值,综合讨论结果可得答案.
解答 解 (1)在(0,+∞)上任取x1.x2,且0<x1<x2,则
f(x1)-f(x2)=($\frac{2}{{x}_{1}}$-1)($\frac{2}{{x}_{2}}$-2)…(2分)
=$\frac{2(x2-x1)}{x1x2}$,…(4分)
∵0<x1<x2,
∴x1x2>0,x2-x1>0,
∴f(x1)-f(x2)>0,…(6分)
即f(x1)>f(x2),
∴f(x)在(0,+∞)上是减函数…(7分)
(2)设x<0,则-x>0,…
∴f(-x)=-$\frac{2}{x}$-1,…(2分)
又f(x)为奇函数,
∴f(-x)=-f(x)=-$\frac{2}{x}$-1,…(4分)
即f(x)=$\frac{2}{x}$+1(x<0)…(6分)
(3)$f(x)=\left\{\begin{array}{l}\frac{2}{x}-1(x>0)\\ 0(x=0)\\ \frac{2}{x}+1(x<0)\end{array}\right\}$…(3分)
当a>0时,$\frac{2}{a}-1=3⇒a=\frac{1}{2}$…(5分)
当a<0时,$\frac{2}{a}+1=3⇒a=1$(舍)…(7分)
点评 本题考查的知识点是分段函数的应用,函数的单调性,函数的奇偶性,是函数图象和性质的综合应用,难度中档.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.经过点P(-3,0),Q(0,-2)的椭圆的标准方程是( )
| A. | $\frac{x^2}{9}+\frac{y^2}{4}=1$ | B. | $\frac{x^2}{4}+\frac{y^2}{9}=1$ | C. | $\frac{x^2}{3}+\frac{y^2}{2}=1$ | D. | $\frac{x^2}{2}+\frac{y^2}{3}=1$ |
1.已知函数y=f(x)是R上的偶函数,且在(-∞,0]上是减函数,若f(a)≥f(2),则实数a的取值范围是( )
| A. | (-∞,2] | B. | (-∞,-2]∪[2,+∞) | C. | [-2,+∞) | D. | [-2,2] |
18.若a>b>0,则( )
| A. | ab<b2 | B. | ($\frac{1}{2}$)a>($\frac{1}{2}$)b | ||
| C. | log${\;}_{\frac{1}{2}}$a>log${\;}_{\frac{1}{2}}$b | D. | a2>b2 |
15.如图,在圆O中,弦AB的长是6,则$\overrightarrow{AO}$•$\overrightarrow{AB}$的值是( )
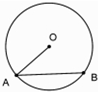

| A. | 18 | B. | -18 | C. | 36 | D. | 不能确定 |