题目内容
下列函数中既是偶函数,又是区间(-1,0)上的减函数的是( )
| A.y=cosx | B.y=-|x-1| | C.y=ln | D.y=ex+e-x |
D
解析试题分析:由偶函数定义:任意的x满足f(-x)=f(x),可以排除答案B和C,又因为y=cosx在区间(-1,0)上的増函数,所以答案是D.
考点:函数的性质.

练习册系列答案
相关题目
已知 ,
, ,规定:当
,规定:当 时,
时,  ;当
;当 时,
时,  ,则
,则 ( )
( )
A.有最小值 ,最大值1 ,最大值1 | B.有最大值1,无最小值 |
C.有最小值 ,无最大值 ,无最大值 | D.有最大值 ,无最小值 ,无最小值 |
已知
 ,定义
,定义 ,其中
,其中 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
如果函数 的图像与曲线
的图像与曲线 恰好有两个不同的公共点,则实数
恰好有两个不同的公共点,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
下列函数中,与函数 的奇偶性、单调性均相同的是( )
的奇偶性、单调性均相同的是( )
A. | B. | C. | D. |
在实数的原有运算法则中,我们补充定义新运算“⊕”;当a≥b时,a⊕b=a;当a<b时,a⊕b=b2,函数f(x)=(1⊕x)·x(其中“·”仍为通常的乘法),则函数f(x)在[0,2]上的值域为( )
| A.[0,4] | B.[1,4] | C.[0,8] | D.[1,8] |
已知符号函数sgn(x)= 则函数f(x)=sgn(lnx)-lnx的零点个数为( )
则函数f(x)=sgn(lnx)-lnx的零点个数为( )
| A.1 | B.2 | C.3 | D.4 |
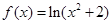 的图象大致是( )
的图象大致是( )