题目内容
已知函数 .
.
(1)求函数 在区间
在区间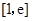 上的最大、最小值;
上的最大、最小值;
(2)求证:在区间 上,函数
上,函数 的图象在函数
的图象在函数 的图象的下方.
的图象的下方.
(1)函数 在区间
在区间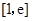 上的最大值为
上的最大值为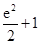 ,最小值为
,最小值为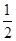 ;
;
(2)要证明在区间 上,函数
上,函数 的图象在函数
的图象在函数 的图象的下方,只要证明前者的最小值大于后者的最大值即可。
的图象的下方,只要证明前者的最小值大于后者的最大值即可。
解析试题分析:解:(1)由已知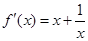 , 1分
, 1分
当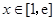 时,
时,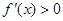 ,所以函数
,所以函数 在区间
在区间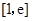 上单调递增, 3分
上单调递增, 3分
所以函数 在区间
在区间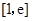 上的最大、最小值分别为
上的最大、最小值分别为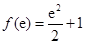 ,
,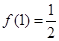 ,所以函数
,所以函数 在区间
在区间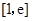 上的最大值为
上的最大值为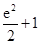 ,最小值为
,最小值为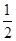 ; 6分
; 6分
(2)证明:设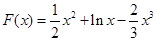 ,则
,则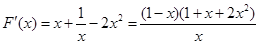 .…8分
.…8分
因为 ,所以
,所以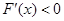 ,所以函数
,所以函数 在区间
在区间 上单调递减, ……9分
上单调递减, ……9分
又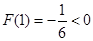 ,所以在区间
,所以在区间 上,
上,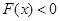 ,即
,即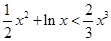 ,
,
所以在区间 上函数
上函数 的图象在函数
的图象在函数 图象的下方.………13分
图象的下方.………13分
考点:导数的运用
点评:解决的关键是利用导数的符号判定函数单调性,并能结合极值得到最值,进而得到图象之间的关系,属于基础题。

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
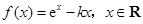
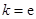 ,试确定函数
,试确定函数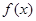 的单调区间;
的单调区间;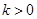 ,且对于任意
,且对于任意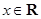 ,
,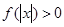 恒成立,试确定实数
恒成立,试确定实数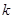 的取值范围;
的取值范围;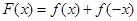 ,求证:
,求证: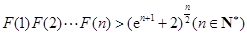 .
.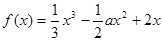 ,讨论
,讨论 的单调性.
的单调性. ,其中
,其中 .
. 在区间(1,2)上不是单调函数,试求
在区间(1,2)上不是单调函数,试求 的取值范围;
的取值范围; ,如果存在
,如果存在 ,使得函数
,使得函数
 在
在 处取得最小值,试求
处取得最小值,试求 的最大值.
的最大值. 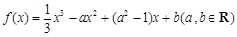
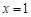 为
为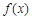 的极值点,求
的极值点,求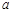 的值;
的值;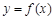 的图象在点
的图象在点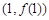 处的切线方程为
处的切线方程为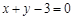 ,求
,求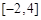 上的最大值;
上的最大值;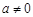 时,若
时,若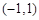 上不单调,求
上不单调,求 其中
其中 ,曲线
,曲线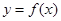 在点
在点 处的切线垂直于
处的切线垂直于 轴.
轴. 的值;
的值; 的极值.
的极值.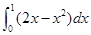 (2)
(2)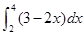
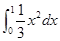 (4)
(4)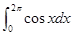
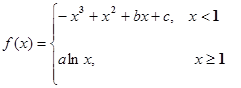 的图像过坐标原点
的图像过坐标原点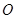 ,且在点
,且在点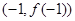 处的切线的斜率是
处的切线的斜率是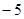 .
.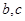 的值;
的值;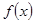 在区间
在区间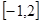 上的最大值;
上的最大值;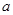 ,曲线
,曲线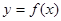 上是否存在两点
上是否存在两点 ,使得
,使得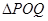 是以
是以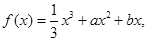 且
且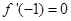
 的代数式表示
的代数式表示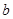 ;
; 的单调区间;
的单调区间; 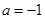 ,设函数
,设函数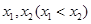 处取得极值,记点
处取得极值,记点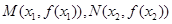 ,证明:线段
,证明:线段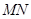 与曲线
与曲线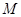 、
、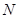 的公共点;
的公共点;