题目内容
已知函数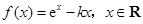
(Ⅰ)若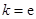 ,试确定函数
,试确定函数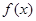 的单调区间;
的单调区间;
(Ⅱ)若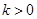 ,且对于任意
,且对于任意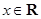 ,
,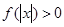 恒成立,试确定实数
恒成立,试确定实数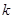 的取值范围;
的取值范围;
(Ⅲ)设函数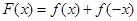 ,求证:
,求证: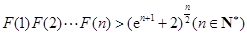 .
.
(1)增区间是 ,减区间是
,减区间是
(2)
(3)构造函数 ,
,
 ,
,
则放缩法得到证明。
解析试题分析:解:(Ⅰ)由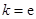 得
得 ,所以
,所以 .
.
由 得
得 ,故
,故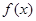 的单调递增区间是
的单调递增区间是 ,
,
由 得
得 ,故
,故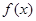 的单调递减区间是
的单调递减区间是 .
.
(Ⅱ)由 可知
可知 是偶函数.
是偶函数.
于是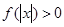 对任意
对任意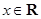 成立等价于
成立等价于 对任意
对任意 成立.
成立.
由 得
得 .
.
①当 时,
时, .
.
此时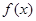 在
在 上单调递增.故
上单调递增.故 ,符合题意.
,符合题意.
②当 时,
时, .
.
当 变化时
变化时 的变化情况如下表:
的变化情况如下表:
由此可得,在







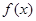
单调递减 极小值 单调递增  上,
上, .
.
依题意, ,又
,又 .
.
综合①,②得,实数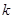 的取值范围是
的取值范围是 .
.
(Ⅲ) ,
,


练习册系列答案
相关题目
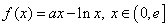 ,其中
,其中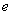 是自然常数,
是自然常数,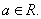
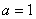 时,
时,  的单调性、极值;
的单调性、极值; ,使
,使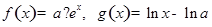 ,其中
,其中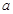 为常数,且函数
为常数,且函数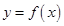 和
和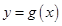 的图象在其与坐标轴的交点处的切线互相平行,求此时平行线的距离。
的图象在其与坐标轴的交点处的切线互相平行,求此时平行线的距离。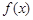 =x+ax2+blnx,曲线y=
=x+ax2+blnx,曲线y=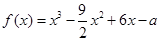 .
.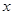 ,
,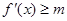 恒成立,求
恒成立,求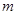 的最大值;
的最大值;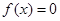 有且仅有一个实根,求
有且仅有一个实根,求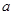 的取值范围.
的取值范围.
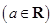 .
.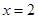 为
为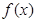 的极值点,求实数
的极值点,求实数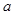 的值;
的值;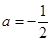 时,方程
时,方程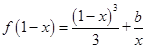 有实根,求实数
有实根,求实数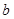 的最大值。
的最大值。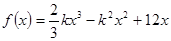 ,是否存在实数
,是否存在实数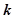 ,使函数在
,使函数在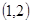 上递减,在
上递减,在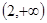 上递增?若存在,求出所有
上递增?若存在,求出所有
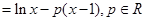
 =
=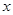
 ,求证:当
,求证:当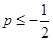 时,有
时,有 成立
成立 .
. 在区间
在区间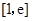 上的最大、最小值;
上的最大、最小值; 上,函数
上,函数 的图象的下方.
的图象的下方.