题目内容
已知函数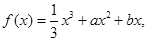 且
且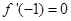
(Ⅰ)试用含 的代数式表示
的代数式表示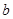 ;
;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)令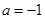 ,设函数
,设函数 在
在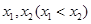 处取得极值,记点
处取得极值,记点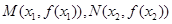 ,证明:线段
,证明:线段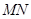 与曲线
与曲线 存在异于
存在异于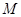 、
、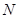 的公共点;
的公共点;
(Ⅰ)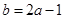 ;(Ⅱ)当
;(Ⅱ)当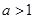 时,函数
时,函数 的单调增区间为
的单调增区间为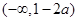 和
和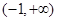 ,单调减区间为
,单调减区间为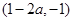 ;当
;当 时,函数
时,函数 的单调增区间为R;当
的单调增区间为R;当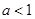 时,函数
时,函数 的单调增区间为
的单调增区间为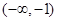 和
和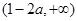 ,单调减区间为
,单调减区间为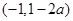
(Ⅲ)易得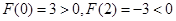 ,而
,而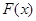 的图像在
的图像在 内是一条连续不断的曲线,
内是一条连续不断的曲线,
故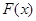 在
在 内存在零点
内存在零点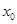 ,这表明线段
,这表明线段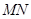 与曲线
与曲线 有异于
有异于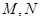 的公共点
的公共点
解析试题分析:解法一:(Ⅰ)依题意,得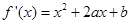
由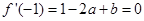 得
得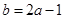
(Ⅱ)由(Ⅰ)得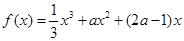
故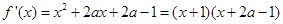
令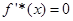 ,则
,则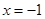 或
或
①当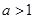 时,
时,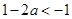
当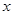 变化时,
变化时,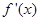 与
与 的变化情况如下表:
的变化情况如下表:
由此得,函数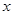
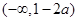
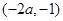
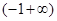
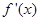
+ — + 
单调递增 单调递减 单调递增  的单调增区间为
的单调增区间为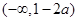 和
和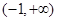 ,单调减区间为
,单调减区间为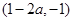
②由 时,
时,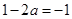 ,此时,
,此时,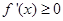 恒成立,且仅在
恒成立,且仅在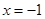 处
处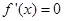 ,故函数
,故函数 的单调区间为R
的单调区间为R
③当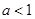 时,
时,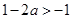 ,同理可得函数
,同理可得函数 的单调增区间为
的单调增区间为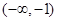 和
和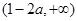 ,单调减区间为
,单调减区间为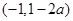
综上:
当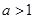 时,函数
时,函数 的单调增区间为
的单调增区间为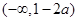 和
和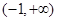 ,单调减区间为
,单调减区间为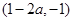 ;
;
当 时,函数
时,函数 的单调增区间为R;
的单调增区间为R;
当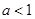 时,函数
时,函数 的单调增区间为
的单调增区间为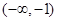 和
和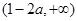 ,单调减区间为
,单调减区间为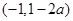
(Ⅲ)当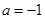 时,得
时,得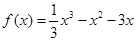
由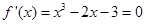

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
. 在区间
在区间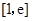 上的最大、最小值;
上的最大、最小值; 上,函数
上,函数 的图象的下方.
的图象的下方.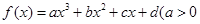 的零点的集合为{0,1},且
的零点的集合为{0,1},且 是f(x)的一个极值点。
是f(x)的一个极值点。 的值;
的值; (其中e为自然对数)
(其中e为自然对数) 的极值。
的极值。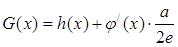 (常数a>0),当x>1时,求函数G(x)的单调区间,并在极值存在处求极值。
(常数a>0),当x>1时,求函数G(x)的单调区间,并在极值存在处求极值。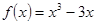 。
。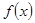 的单调区间;
的单调区间;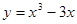 上一点
上一点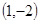 的切线方程。
的切线方程。
 R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围;
R,对任意的a∈(-l,1),总存在xo∈[1,e],使得不等式ma - (xo)<0成立,求实数m的取值范围; ∈N*).
∈N*).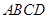 缺损一角(图中的阴影部分),边缘线
缺损一角(图中的阴影部分),边缘线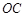 是以直线
是以直线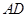 为对称轴,以线段
为对称轴,以线段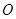 为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.
为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.
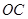 的方程;
的方程;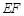 ,使得剩余部分即直角梯形
,使得剩余部分即直角梯形 的面积最大?
的面积最大? .
. 时,求证:函数
时,求证:函数 在
在 上单调递增;
上单调递增; 有三个零点,求
有三个零点,求 的值;
的值; ,使得
,使得 ,试求
,试求 的取值范围。
的取值范围。 ,其图象在点
,其图象在点 处的切线方程为
处的切线方程为 .
. 的值;
的值; 的单调区间,并求出
的单调区间,并求出 上的最大值.
上的最大值.