题目内容
6.设双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的下焦点为F(0,-c),直线y=kx-c与圆x2+y2=a2相切于点M,与双曲线的上支交于点N,若∠MOF=∠MON(O是坐标原点),则此双曲线的离心率为( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\frac{1+\sqrt{5}}{2}$ | D. | $\frac{1+\sqrt{3}}{2}$ |
分析 设双曲线的上焦点为F',连接NF',可得NF'与OM平行,即有NF⊥NF',由中位线定理可得|NF'|=2a,运用双曲线的定义,再由勾股定理和离心率公式,即可得到所求.
解答 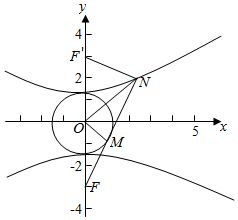 解:设双曲线的上焦点为F',连接NF',
解:设双曲线的上焦点为F',连接NF',
由直线y=kx-c与圆x2+y2=a2相切于点M,
由OM⊥NF,且∠MOF=∠MON,
可得M为NF'的中点,由中位线定理可得NF⊥NF',
且|NF|'=2|OM|=2a,
由双曲线的定义可得|NF|=2a+2a=4a,
在直角三角形NFF'中,可得
(2c)2=4a2+(2a+2a)2,
即有4c2=20a2,
由c2=5a2,
即为c=$\sqrt{5}$a,
则e=$\frac{c}{a}$=$\sqrt{5}$.
故选:B.
点评 本题考查双曲线的离心率的求法,注意运用双曲线的定义和中位线定理,以及勾股定理,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
16.据统计2016年“十一”黄金周哈尔滨太阳岛每天的游客人数服从正态分布N(2000,1002),则在此期间的某一天,太阳岛的人数不超过2300的概率为( )
附;若X~N(μ,σ2)
$\begin{array}{l}P(μ-σ<x≤μ+σ)=0.6826\\ P(μ-2σ<x≤μ+2σ)=0.9544\\ P(μ-3σ<x≤μ+3σ)=0.9974\end{array}$.
附;若X~N(μ,σ2)
$\begin{array}{l}P(μ-σ<x≤μ+σ)=0.6826\\ P(μ-2σ<x≤μ+2σ)=0.9544\\ P(μ-3σ<x≤μ+3σ)=0.9974\end{array}$.
| A. | 0.4987 | B. | 0.8413 | C. | 0.9772 | D. | 0.9987 |
17.已知O、A、B三点不共线,P为该平面内一点,且$\overrightarrow{OP}=\overrightarrow{OA}+\frac{{\overrightarrow{AB}}}{{|{\overrightarrow{AB}}|}}$,则( )
| A. | 点P在线段AB 上 | B. | 点P在线段AB的延长线上 | ||
| C. | 点P在线段AB的反向延长线上 | D. | 点P在射线AB上 |
1.已知$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-1,3),则|2$\overrightarrow{a}$-$\overrightarrow{b}$|=( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 10 | D. | $\sqrt{10}$ |
18.为了判断高中三年级学生选修文理科是否与性别有关,现随机抽取50名学生,得到2×2列联表:
已知P(K2≥3.841)≈0.05,P(K2≥5.024)≈0.025.
根据表中数据,得到K2=$\frac{50×(13×20-10×7)2}{23×27×20×30}$≈4.844,则认为选修文理科与性别有关系出错的可能性约为5%.
| 理科 | 文科 | 总计 | |
| 男 | 13 | 10 | 23 |
| 女 | 7 | 20 | 27 |
| 总计 | 20 | 30 | 50 |
根据表中数据,得到K2=$\frac{50×(13×20-10×7)2}{23×27×20×30}$≈4.844,则认为选修文理科与性别有关系出错的可能性约为5%.
15. 设函数f(x)在R上可导,其导函数为f′(x),如图是函数g(x)=xf′(x)的图象,则f(x)的极值点是( )
设函数f(x)在R上可导,其导函数为f′(x),如图是函数g(x)=xf′(x)的图象,则f(x)的极值点是( )
 设函数f(x)在R上可导,其导函数为f′(x),如图是函数g(x)=xf′(x)的图象,则f(x)的极值点是( )
设函数f(x)在R上可导,其导函数为f′(x),如图是函数g(x)=xf′(x)的图象,则f(x)的极值点是( )| A. | 极大值点x=-2,极小值点x=0 | B. | 极小值点x=-2,极大值点x=0 | ||
| C. | 极值点只有x=-2 | D. | 极值点只有x=0 |
 三棱锥A-BCD中,E是BC的中点,且BD=8,CD=6,BC=10,AB=AD=4$\sqrt{2}$.
三棱锥A-BCD中,E是BC的中点,且BD=8,CD=6,BC=10,AB=AD=4$\sqrt{2}$.