题目内容
 如图,三棱锥V-ABC中,VA=VB=AC=BC=2VC,∠ACB=120°.
如图,三棱锥V-ABC中,VA=VB=AC=BC=2VC,∠ACB=120°.(1)求证:AB⊥VC;
(2)求二面角V-AB-C的度数.
考点:二面角的平面角及求法,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(1)取AB中点E,连接VE,CE,由已知条件推导出VE⊥AB,CE⊥AB,从而AB⊥平面VEC,由此能证明AB⊥VC.
(2)由已知得∠VEC为所求二面角V-AB-C的平面角,由此能求出二面角V-AB-C的度数.
(2)由已知得∠VEC为所求二面角V-AB-C的平面角,由此能求出二面角V-AB-C的度数.
解答:
(1)证明:取AB中点E,连接VE,CE,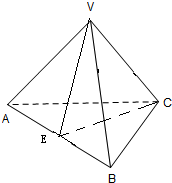
因为VA=VB,所以VE⊥AB,
同理,因为CA=CB,所以CE⊥AB,
又因为VE∩CE=E,
所以AB⊥平面VEC,
又因为VC?平面VEC
所以AB⊥VC.
(2)解:由(1)知∠VEC为所求二面角V-AB-C的平面角,
设VC=a,因为E为中点,AB=AC=2VC=2a,
又因为∠ACB=120°,所以AE=EB=
a,CE=a,VE=a,
因为在△VEC中,VC=a,所以△VEC为等边三角形,
所以∠VEC=60°,所以二面角V-AB-C的度数为60°.

因为VA=VB,所以VE⊥AB,
同理,因为CA=CB,所以CE⊥AB,
又因为VE∩CE=E,
所以AB⊥平面VEC,
又因为VC?平面VEC
所以AB⊥VC.
(2)解:由(1)知∠VEC为所求二面角V-AB-C的平面角,
设VC=a,因为E为中点,AB=AC=2VC=2a,
又因为∠ACB=120°,所以AE=EB=
| 3 |
因为在△VEC中,VC=a,所以△VEC为等边三角形,
所以∠VEC=60°,所以二面角V-AB-C的度数为60°.
点评:本题考查异面直线垂直的证明,考查二面角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
若O为三角形ABC所在平面内的一点,且满足(
-
)•(
+
-2
)=0,则三角形ABC为( )
| OB |
| OC |
| OB |
| OC |
| OA |
| A、正三角形 | B、直角三角形 |
| C、等腰三角形 | D、以上都不对 |