题目内容
如图,圆O1与圆O2的半径都是1, ,过动点P分别作圆O1.圆O2的切线PM、PN(M.N分别为切点),使得
,过动点P分别作圆O1.圆O2的切线PM、PN(M.N分别为切点),使得 试建立适当的坐标系,并求动点P的轨迹方程
试建立适当的坐标系,并求动点P的轨迹方程

解析试题分析:以O1O2的中点O为原点,O1O2所在直线为 轴,建立如图所示
轴,建立如图所示
平面直角坐标系。
则O1(-2,0),O2(2,0),
由已知: ,即PM2=2PN2,
,即PM2=2PN2,
∵两圆的半径都为1,∴ ,
,
设 ,
,
则 ,即
,即 。
。
∴所求轨迹方程为: (或
(或 ).
).
考点:点与圆的位置关系.
点评:本题是典型的求轨迹方程的方法,坐标系的建立是关键,是基础题.

练习册系列答案
相关题目
 的圆心在点
的圆心在点 , 点
, 点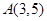 ,求;
,求; 的圆的切线方程;
的圆的切线方程; 点是坐标原点,连结
点是坐标原点,连结 ,
, ,求
,求 的面积
的面积 .
. ,直线
,直线 与圆
与圆 相交于
相交于 两点,且A点在第一象限.
两点,且A点在第一象限. ;
; (
( )是圆
)是圆 关于原点的对称点为
关于原点的对称点为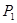 ,点
,点 轴的对称点为
轴的对称点为 ,如果直线
,如果直线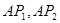 与
与 轴分别交于
轴分别交于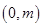 和
和 .问
.问 是否为定值?若是,求出定值,若不是,说明理由.
是否为定值?若是,求出定值,若不是,说明理由. 
 内有一点
内有一点 ,
, 为过点
为过点 且倾斜角为
且倾斜角为 的弦,
的弦, 时,求
时,求 被圆
被圆 所截得的弦长.
所截得的弦长.  ,直线
,直线 .
. 与
与 相切,求
相切,求 的值;
的值; 两点,且
两点,且 (其中
(其中 为坐标原点),若存在,求出
为坐标原点),若存在,求出 过点
过点 ,且与直线
,且与直线 相切于点
相切于点 .
.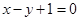 对称的圆
对称的圆 的方程.
的方程.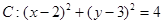 ,直线
,直线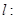
 ,
,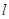 与圆
与圆 恒相交;
恒相交; 时,过圆
时,过圆 作圆的切线
作圆的切线 交直线
交直线 点,
点, 为圆
为圆 的取值范围;
的取值范围; 轴相切,圆心在直线
轴相切,圆心在直线 上,且在直线
上,且在直线 上截得的弦长为
上截得的弦长为 ,求圆C的方程.
,求圆C的方程.