Question

【题目】选修4—4：坐标系与参数方程

已知直线l经过点，倾斜角，圆的极坐标方程为．

（Ⅰ）写出直线l的参数方程，并把圆的方程化为直角坐标方程；

（Ⅱ）设l与圆相交于两点，求点到两点的距离之积．

Answer 1

【答案】（1）；（2）.

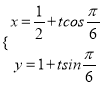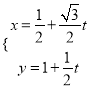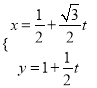【解析】试题分析：（1）由参数方程的概念可以写成l的参数方程为，化简为 (t为参数) ；在两边同时乘以，且ρ2＝x2＋y2，ρcosθ＝x，ρsinθ＝y，∴.（2）在l取一点，用参数形式表示，再代入，得到t2＋t－＝0，|PA|·|PB|＝|t1t2|＝.故点P到点A、B两点的距离之积为.

试题解析：(1)直线l的参数方程为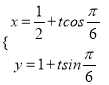,即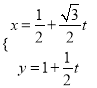 (t为参数)

由,得ρ＝cosθ＋sinθ，所以ρ2＝ρcosθ＋ρsinθ，

∵ρ2＝x2＋y2，ρcosθ＝x，ρsinθ＝y，∴.

(2)把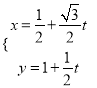代入.

得t2＋t－＝0，|PA|·|PB|＝|t1t2|＝.故点P到点A、B两点的距离之积为.