题目内容
若函数f（x）=loga|x-2|（a＞0，且a≠1）在区间（1，2）上是增函数，则f（x）在区间（2，+∞）上（ ）
| A、是增函数且有最大值 |
| B、是增函数且无最大值 |
| C、是减函数且有最小值 |
| D、是减函数且无最小值 |
考点：对数函数的图像与性质
专题：函数的性质及应用
分析：先求出a的范围，从而得到f（x）在（2，+∞）递减，且不存在最小值，从而得到答案．
解答：
解：x∈（1，2）∴|x-2|=2-x是减函数，而f（x）是增函数，∴0＜a＜1，
x∈（2，+∞）时，|x-2|=x-2是增函数，∴f（x）在0＜a＜1时，是减函数，
且不存在最小值，
故选：D．
x∈（2，+∞）时，|x-2|=x-2是增函数，∴f（x）在0＜a＜1时，是减函数，
且不存在最小值，
故选：D．
点评：本题考查了导数函数的性质，考查了函数的单调性，是一道基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如果一个几何体的三视图如图所示（单位长度：cm），则此几何体的表面积是（ ）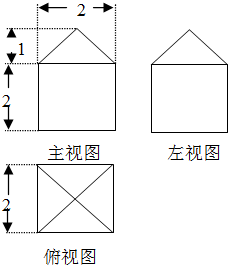
A、（20+4
| ||
| B、21 cm | ||
C、（24+4
| ||
| D、24 cm |
5人站成一排，甲、乙两人相邻的不同站法的种数为（ ）
| A、24 | B、36 | C、48 | D、60 |
设a、b、c分别是△ABC的三个内角A、B、C所对的边，若a=1，b=bc，则“A=30°”是“B=60°”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |