题目内容
已知四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC.
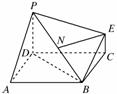
(1)求证:BE∥平面PDA;
(2)若N为线段PB的中点,求证:NE⊥平面PDB.
证明: (1)∵EC∥PD,PD⊂平面PDA,EC⊄平面PDA,
∴EC∥平面PDA,
同理可得BC∥平面PDA.
∵EC⊂平面EBC,BC⊂平面BEC且EC∩BC=C,
∴平面BEC∥平面PDA.
又∵BE⊂平面BEC,∴BE∥平面PDA.

(2)连接AC,交BD于点F,连接NF,
∵F为BD的中点,
∴NF∥PD且NF=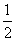 PD,
PD,
又EC∥PD且EC=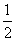 PD,
PD,
∴NF∥EC且NF=EC.
∴四边形NFCE为平行四边形,
∴NE∥FC,
∵PD⊥平面ABCD,AC⊂平面ABCD,∴AC⊥PD,
又DB⊥AC,PD∩BD=D,∴AC⊥平面PDB,
∴NE⊥平面PDB.

练习册系列答案
相关题目
 对一切非零实数x均成立,则实数a的最大值是________.
对一切非零实数x均成立,则实数a的最大值是________. 上随机取两个实数
上随机取两个实数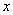 ,
,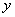 ,则事件“
,则事件“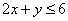 ”的概率为_________.
”的概率为_________.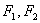 分别是双曲线
分别是双曲线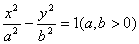 的左右焦点,
的左右焦点,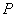 为双曲线右支上一点,
为双曲线右支上一点,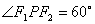 ,
,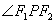 的角平分线
的角平分线 交
交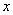 轴于
轴于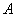 ,
,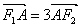 ,则双曲线的离心率为
,则双曲线的离心率为 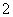 B.
B.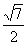 C.
C. D.
D.