若正数a.b满足3+log2a=2+log3b=log6(a+b).则$\frac{1}{a}$+$\frac{1}{b}$的值为72．题目和参考答案——青夏教育精英家教网—

题目内容

14．若正数a，b满足3+log₂a=2+log₃b=log₆（a+b），则$\frac{1}{a}$+$\frac{1}{b}$的值为72．

分析令3+log₂a=2+log₃b=log₆（a+b）=x，变形后化对数式为指数式，代入$\frac{1}{a}$+$\frac{1}{b}$求得答案．

解答解：由3+log₂a=2+log₃b=log₆（a+b），
∴设3+log₂a=2+log₃b=log₆（a+b）=x，
则a=2^x-3，b=3^x-2，a+b=6^x，
∴$\frac{1}{a}$+$\frac{1}{b}$=$\frac{a+b}{ab}=\frac{{6}^{x}}{{2}^{x-3}•{3}^{x-2}}=72$．
故答案为：72．

点评本题考查代数和的值的求法，关键是对对数性质的合理运用，是基础题．

练习册系列答案

易考教育书系中考导航中考试卷汇编系列答案

长江新浪学考联通给力100学期总复习寒假长江出版社系列答案

寒假作业与生活陕西师范大学出版总社系列答案

假期总动员学期系统复习系列答案

寒假作业河北美术出版社系列答案

寒假作业本希望出版社系列答案

5．

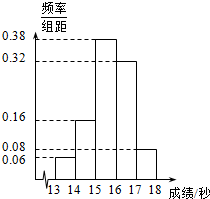2015年08月22日至2015年08月30日在北京举行国际田联世界田径锦标赛，其中50名运动员在一次百米测试中，成绩全部介于13秒与18秒之间，来自牙买加的运动员博尔特取得最好的成绩．将测试结果按如下方式分成五组：第一组[13，14），第二组[14，15）…第五组[17，18]，
如图是按上述分组方法得到的频率分布直方图
（1）若成绩大于或等于14秒且小于16秒的认为良好，求50名运动员在这次百米测试中成绩良好的人数；
（2）设m，n表示50名运动员中某两名运动员的百米测试成绩，且已知m，n∈[13，14）∪[17，18]，求事件“|m-n|＞1”的概率．

2．从2个红球，2个黄球，1个白球中随机取出两个球，则两球颜色不同的概率是$\frac{4}{5}$．

9．已知集合A={x|0＜log₂x＜2}，B={y|y=3^x+2，x∈R}，则A∩B=（　　）

19．设f（x）=|x-3|+|x-4|
（Ⅰ）求函数g（x）=$\sqrt{2-f（x）}$的定义域；
（Ⅱ）若对任意的实数x，不等式f（x）≥a²-a-1恒成立，求实数a的取值范围．

6．已知函数f（x）=ln（1+x）-$\frac{x}{1+x}$（a∈R，a≠0）．
（1）求f （x）的单调区间；
（2）证明：?n∈N^*，有$\frac{1}{n+1}＜ln（\frac{1}{n}+1）＜\frac{1}{n}$；
（3）若a_n=1+$\frac{1}{2}+…+\frac{1}{n}$-lnn，证明：?n∈N^*，有a_n＞a_n+1＞0．

3．设X为随机变量，从棱长为a的正方体ABCD-A₁B₁C₁D₁的八个顶点中任取四个点，当四点共面时，X=0；当四点不共面时，X的值为四点组成的四面体的体积
（1）求X=0的概率；
（2）求X的分布列，并求其数学期望．

4．函数f（x）=-x²+3x+1，x∈[m，m+1]，求：
（1）f（x）的最小值g（m）；
（2）g（m）的最大值．

试题分类