题目内容
己知向量a=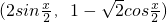 ,b=
,b=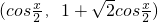 ,函数
,函数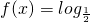 (a•b).
(a•b).
(Ⅰ)求函数f(x)的定义域和值域;
(Ⅱ)求函数f(x)的单调区间.
解:(Ⅰ)∵ =
=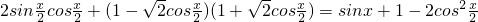
=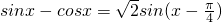 .
.
由 ,
,
得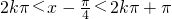 ,
,
即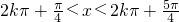 ,k∈Z.
,k∈Z.
∴f(x)的定义域是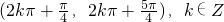 .
.
∵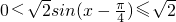 ,则
,则 ,
,
∴f(x)的值域是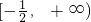 .
.
(Ⅱ)由题设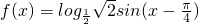 .
.
若f(x)为增函数,则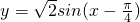 为减函数,
为减函数,
∴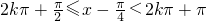 ,
,
即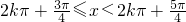 ,
,
∴f(x)的递增区间是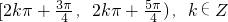 .
.
若f(x)为减函数,则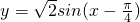 为增函数,
为增函数,
∴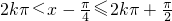 ,即
,即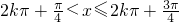 ,
,
∴f(x)的递减区间是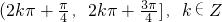 .
.
分析:(1)首先要对所给的函数式进行整理,根据两个向量的数量积,得到有关三角函数的式子,变成最简形式,求出函数的定义域和值域,定义域是对于对数的真数的范围要求.
(2)本题是一个复合函数的单调性问题,解题依据是同增异减,因为外层函数是一个减函数,所以内层函数的单调性同整个函数的单调性相反.
点评:这是一种可以作为高考题出现的题目,把向量同三角函数结合起来,以向量为载体,题目中还考到复合函数的单调性,解题时容易出错,这是一道中档题,在高考题目中的地位较高.
 =
=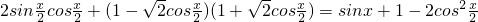
=
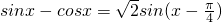 .
.由
 ,
,得
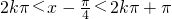 ,
,即
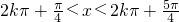 ,k∈Z.
,k∈Z.∴f(x)的定义域是
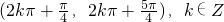 .
.∵
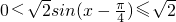 ,则
,则 ,
,∴f(x)的值域是
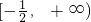 .
.(Ⅱ)由题设
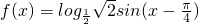 .
.若f(x)为增函数,则
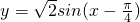 为减函数,
为减函数,∴
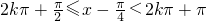 ,
,即
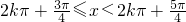 ,
,∴f(x)的递增区间是
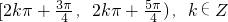 .
.若f(x)为减函数,则
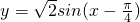 为增函数,
为增函数,∴
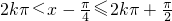 ,即
,即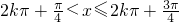 ,
,∴f(x)的递减区间是
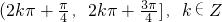 .
.分析:(1)首先要对所给的函数式进行整理,根据两个向量的数量积,得到有关三角函数的式子,变成最简形式,求出函数的定义域和值域,定义域是对于对数的真数的范围要求.
(2)本题是一个复合函数的单调性问题,解题依据是同增异减,因为外层函数是一个减函数,所以内层函数的单调性同整个函数的单调性相反.
点评:这是一种可以作为高考题出现的题目,把向量同三角函数结合起来,以向量为载体,题目中还考到复合函数的单调性,解题时容易出错,这是一道中档题,在高考题目中的地位较高.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
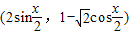 ,b=
,b=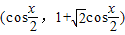 ,函数
,函数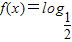 .
.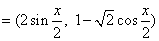 ,b
,b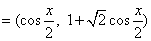 ,函数
,函数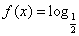 (a·b).
(a·b).