题目内容
16.已知圆O为Rt△ABC的外接圆,AB=AC,BC=4,过圆心O的直线l交圆O于P,Q两点,则$\overrightarrow{BP}•\overrightarrow{CQ}$的取值范围是( )| A. | [-8,-1] | B. | [-8,0] | C. | [-16,-1] | D. | [-16,0] |
分析 以O为坐标原点,BC所在的直线为x轴,BC的中垂线为y轴建立直角坐标系,则△ABC外接圆的圆心是BC的中点,半径r=$\frac{1}{2}$BC,写出圆O的方程以及$\overrightarrow{BP}$、$\overrightarrow{CQ}$的坐标表示,求出$\overrightarrow{BP}$•$\overrightarrow{CQ}$的取值范围即可.
解答 解:【解法一】以O为坐标原点,BC所在的直线为x轴,BC的中垂线为y轴,
建立直角坐标系,如图所示;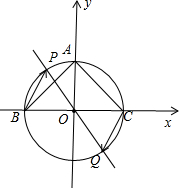
在Rt△ABC中,AB=AC,BC=4,
所以△ABC的外接圆圆心是BC的中点,半径为r=$\frac{1}{2}$BC=2,
所以A(0,2),B(-2,0),C(2,0),
圆O的方程为:x2+y2=4;
当直线PQ的斜率不存在时,有P(0,2),Q(0,-2),
$\overrightarrow{BP}$=(2,2),$\overrightarrow{CQ}$=(-2,-2),则$\overrightarrow{BP}$•$\overrightarrow{CQ}$=-4-4=-8;
当直线PQ的斜率存在时,设直线l为:y=kx,
代入圆的方程可得P(-$\frac{2}{\sqrt{1{+k}^{2}}}$,-$\frac{2k}{\sqrt{1{+k}^{2}}}$),Q($\frac{2}{\sqrt{1{+k}^{2}}}$,$\frac{2k}{\sqrt{1{+k}^{2}}}$),
则$\overrightarrow{BP}$=(2-$\frac{2}{\sqrt{1{+k}^{2}}}$,-$\frac{2k}{\sqrt{1{+k}^{2}}}$),$\overrightarrow{CQ}$=($\frac{2}{\sqrt{1{+k}^{2}}}$-2,$\frac{2k}{\sqrt{1{+k}^{2}}}$),
所以$\overrightarrow{BP}$•$\overrightarrow{CQ}$=(2-$\frac{2}{\sqrt{1{+k}^{2}}}$)($\frac{2}{\sqrt{1{+k}^{2}}}$-2)+(-$\frac{2k}{\sqrt{1{+k}^{2}}}$)$\frac{2k}{\sqrt{1{+k}^{2}}}$
=-8+$\frac{8}{\sqrt{1{+k}^{2}}}$,
由1+k2≥1可得0<$\frac{8}{\sqrt{1{+k}^{2}}}$≤8,
所以-8<-8+$\frac{8}{\sqrt{1{+k}^{2}}}$≤0;
又题目中没有要求P、Q的具体位置,所以P、Q坐标互换时,
比如,当k=0时,若P(2,0),Q(-2,0),
则向量$\overrightarrow{BP}$=(4,0),向量$\overrightarrow{CQ}$=(-4,0),
所以$\overrightarrow{BP}$•$\overrightarrow{CQ}$=-16.
故选:D.
【解法二】以O为坐标原点,BC所在的直线为x轴,BC的中垂线为y轴,
建立直角坐标系,如图所示;
在Rt△ABC中,AB=AC,BC=4,
所以△ABC的外接圆圆心是BC的中点,半径为r=$\frac{1}{2}$BC=2,
所以A(0,2),B(-2,0),C(2,0),
圆O的方程为:x2+y2=4;
设P(2sinθ,2cosθ),Q(-2sinθ,-2cosθ),
把$\overrightarrow{BP}•\overrightarrow{CQ}$转化为三角函数计算更简单.
点评 本题考查了平面向量的数量积与坐标运算问题,以及直线与圆的位置关系和不等式的性质问题,是综合题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
| A. | {0} | B. | {2} | C. | ∅ | D. | {-2,0,2} |