题目内容
(本小题满分10分)选修4—5:不等式选讲
已知函数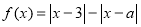 .
.
(1)当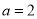 时,解不等式
时,解不等式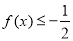 ;
;
(2)若存在实数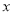 ,使得不等式
,使得不等式 成立,求实数
成立,求实数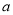 的取值范围.
的取值范围.
(1) 或
或 或
或 ;(2)实数
;(2)实数 的取值范围是
的取值范围是 .
.
【解析】
试题分析:(1)运用函数的零点分区间,讨论当 时,当
时,当 时,当
时,当 时,化简不等式解得,最后求并集即可;(2)由题意知这是一个存在性的问题,须求出不等式左边的最大值,可运用绝对值不等式的性质可得最大值,再令其大于等于
时,化简不等式解得,最后求并集即可;(2)由题意知这是一个存在性的问题,须求出不等式左边的最大值,可运用绝对值不等式的性质可得最大值,再令其大于等于 ,即可解出实数
,即可解出实数 的取值范围.
的取值范围.
试题分析:(1)∵ ,∴
,∴ , 1分
, 1分
∴ 等价于
等价于 或
或 或
或 , 3分
, 3分
解得 或
或 ,∴不等式的解集为
,∴不等式的解集为 ; 5分
; 5分
(2)由不等式性质可知 , 8分
, 8分
∴若存在实数 ,使得不等式
,使得不等式 成立,则
成立,则 ,解得
,解得 ,
,
∴实数 的取值范围是
的取值范围是 . 10分
. 10分
考点:1.绝对值不等式;2.存在性问题的处理方法.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
(本小题满分12分)心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学(男30女20),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)
几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
(1)能否据此判断有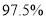 的把握认为视觉和空间能力与性别有关?
的把握认为视觉和空间能力与性别有关?
(2)经过多次测试后,甲每次解答一道几何题所用的时间在5~7分钟,乙每次解答一道几何题所用的时
间在6~8分钟,现甲、乙各解同一道几何题,求乙比甲先解答完的概率.
(3)现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、乙两女生被抽到的人数为 ,求
,求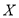 的分布列及数学期望
的分布列及数学期望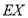 .
.
下面临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
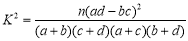 .
.
 上的奇函数
上的奇函数 =
= 的图象如图所示,则
的图象如图所示,则 的大小关系是
的大小关系是 
 B.
B.
 D.
D.
 是偶函数,
是偶函数, 且当
且当 时,其导函数
时,其导函数 满足
满足 ,若
,若 ,则 B
,则 B



 的最大值为 .
的最大值为 . 的图象沿
的图象沿 轴向右平移
轴向右平移 个单位后,得到一个偶函数的图象,则
个单位后,得到一个偶函数的图象,则 的取值不可能是( )
的取值不可能是( ) B.
B. C.
C. D.
D.
 中,
中, ,
, ,
, 、
、 分别为
分别为 和
和 上的点,且
上的点,且 .
.
 时,
时, ;
; 为何值时,三棱锥
为何值时,三棱锥 的体积最小,并求出最小体积.
的体积最小,并求出最小体积. 是定义在
是定义在 上周期为
上周期为 的函数,且对任意的实数
的函数,且对任意的实数 ,恒有
,恒有 ,当
,当 ,
, .若
.若 在
在 有且仅有三个零点,则
有且仅有三个零点,则 的取值范围为( )
的取值范围为( ) B.
B. C.
C. D.
D.


 为虚数单位,则
为虚数单位,则 =( )
=( ) C.
C.  D.
D. 