题目内容
已知函数 是偶函数,
是偶函数, 且当
且当 时,其导函数
时,其导函数 满足
满足 ,若
,若 ,则 B
,则 B
A.
B.
C.
D.
B
【解析】
试题分析:根据函数的性质可知: 是偶函数,其图像关于直线
是偶函数,其图像关于直线 对称,则
对称,则 是由
是由 的图像向右平移
的图像向右平移 个单位得到的,所以函数的
个单位得到的,所以函数的 图像关于直线
图像关于直线 ,再根据原函数的导函数的关系及
,再根据原函数的导函数的关系及 可知,当
可知,当 时
时 得到:
得到: 在区间
在区间 单调递增,同理
单调递增,同理 在区间
在区间 单调递减,所以要比较
单调递减,所以要比较 (其中
(其中 )的大小,根据图像的对称性和单调性显然,只要比较
)的大小,根据图像的对称性和单调性显然,只要比较 ,所以
,所以
 ,显然
,显然 均在递增区间
均在递增区间 ,且
,且 ,所以
,所以 ,答案为B.
,答案为B.
考点:1.函数奇偶性;2.函数的图像变换;3.比较大小.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,集合
,集合 ,则
,则 =( )
=( ) B.
B. C.
C. D.
D.
 满足
满足 ,
, ,若对任意的自然数
,若对任意的自然数 ,恒有
,恒有 ,则
,则 的取值范围为 .
的取值范围为 .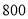 名男生中随机抽取
名男生中随机抽取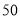 名测量身高,被测学生身高全部介于
名测量身高,被测学生身高全部介于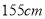 和
和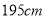 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组 ,第二组
,第二组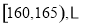 ,第八组
,第八组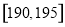 ,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为
,下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为 人。
人。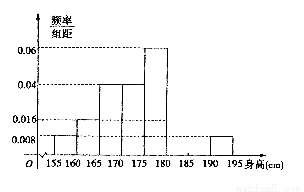
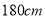 以上(含
以上(含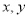 ,事件
,事件 ,事件
,事件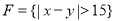 ,求
,求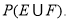
 满足
满足 ,
, ,则向量
,则向量 方向上的投影为 。
方向上的投影为 。 下列结论错误的是( )
下列结论错误的是( ) 的最小正周期为
的最小正周期为
 对称
对称  上是增函数
上是增函数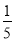 和
和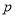 ,若在任意时刻至多有一个系统发生故障的概率为
,若在任意时刻至多有一个系统发生故障的概率为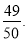
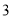 次相互独立的检测中不发生故障的次数为随机变量
次相互独立的检测中不发生故障的次数为随机变量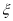 ,求
,求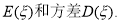
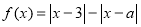 .
.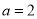 时,解不等式
时,解不等式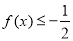 ;
;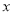 ,使得不等式
,使得不等式 成立,求实数
成立,求实数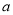 的取值范围.
的取值范围.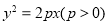 ,过抛物线上一点
,过抛物线上一点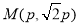 和抛物线的焦点
和抛物线的焦点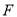 作直线
作直线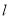 交抛物线于另一点
交抛物线于另一点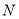 ,则
,则 ( )
( )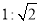 B.
B.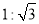 C.
C.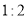 D.
D.