题目内容
4.已知抛物线的顶点在原点,对称轴是x轴,抛物线上的点M(-3,m)到焦点的距离等于5,(1)求抛物线的方程.
(2)过点P(-4,1)作直线l交抛物线与A,B两点,使弦AB恰好被P点平分,求直线l的方程.
分析 根据题意可设抛物线的方程为:y2=-2px,利用抛物线的定义求得p的值,得到抛物线的方程;
(2)由题意可设AB的方程为x=my-4-m,代入抛物线的标准方程为y2=-8x,由y1+y2=-8m=2,求得m的值,从而得到AB的方程.
解答 解:(1)由题意可设抛物线方程:y2=-2px,
焦点坐标为(-$\frac{p}{2}$,0),准线为:x=$\frac{p}{2}$,
∵抛物线上的点M(-3,m)到焦点的距离是5.
由抛物线的定义可得,$\frac{p}{2}$+3=5,
解得p=4,
即有抛物线方程为y2=-8x;
(2)由题意可设AB的方程为x=my-4-m,代入抛物线的标准方程为y2=-8x,
可得y2+8my-32-8m=0,∴y1+y2=-8m=2,∴m=-$\frac{1}{4}$,∴AB的方程为4x+y+15=0.
点评 本题考查抛物线的标准方程,直线和圆锥曲线的位置关系,线段的中点公式的应用,得到y1+y2=-8m=2,是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.点M(1,1)到抛物线y=ax2准线的距离为3,则a的值为( )
| A. | $\frac{1}{8}$ | B. | 8 | C. | $\frac{1}{8}或-\frac{1}{16}$ | D. | $\frac{1}{8}$或-16 |
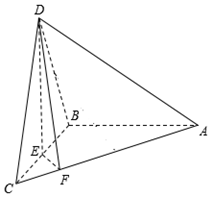 如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC,
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC,