题目内容
如图,在三棱柱ABC—A1B1C1中,AA1⊥平面ABC,AB⊥BC,且AB =BC=2,点N为B1C1的中点,点P在棱A1C1上运动.
=BC=2,点N为B1C1的中点,点P在棱A1C1上运动.
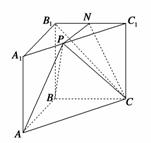
(1)试问点P在何处时,AB∥平面PNC,并证明你的结论;
(2)在(1)的条件下,若AA1<AB,直线B1C与平面BCP所成角的正弦值为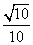 ,求二面角A-BP-C的大小.
,求二面角A-BP-C的大小.
(1)当点P为A1C1的中点时,AB∥平面PNC.
∵P为A1C1的中点,N为B1C1的中点,∴PN∥A1B1∥AB
∵AB⊄平面PNC,PN⊂平面PNC,∴AB∥平面PNC.
(2)设AA1=m,则m<2,∵AB、BC、BB,两两垂直,
∴以B为原点,BA、BC,BB1为x轴、y轴,z轴建立空间直角坐标系,则A(2,0,0),C(0,2,0),B1(0,0,m),A1(2,0,m),C1(0,2,m),
∴P(1,1,m),设平面BCP的法向量n=(x,y,z),
则由n·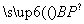 =0,n·
=0,n·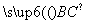 =0,解得y=0,x=-mz,
=0,解得y=0,x=-mz,
令z=0,则n=(-m,0,-1),又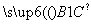 =(0,2,-m),
=(0,2,-m),
直线B1C与平面BCP所成角正弦值为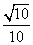 ,
,
∴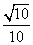 =
=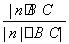 ,解之得m=1
,解之得m=1
∴n=(-1,0,1)
易求得平面ABP的法向量n1=(0,-1,1)
cosα=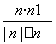 =
= ,设二面角的平面角为θ,则cosθ=-
,设二面角的平面角为θ,则cosθ=- ,∴θ=120°.
,∴θ=120°.

练习册系列答案
相关题目
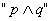 为真是
为真是 为真的充分不必要条件
为真的充分不必要条件 为假的必要不充分条件
为假的必要不充分条件
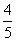 B.
B.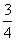 C.
C.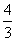 D.
D.
 1时,有如下表达式:
1时,有如下表达式: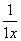 ,
,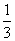 ×(
×(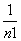 ×(
×(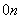 ×
×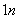 ×(
×(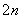 ×(
×(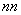 ×(
×(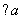 =(cos40,sin40),
=(cos40,sin40), =(cos80,-sin80),则
=(cos80,-sin80),则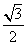 C.-
C.- 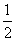 D.
D.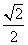
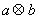 为执行如图所示的程序框图输出的s值,则
为执行如图所示的程序框图输出的s值,则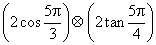 的值为( )
的值为( )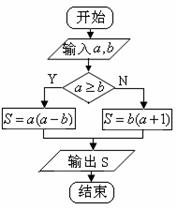
 ,则
,则
 B.
B.
 D.
D.
 的前
的前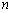 项和为
项和为 ,且满足对
,且满足对 (
( ).
). ,
, ,
, 的值;
的值; ,并证明你的结论;
,并证明你的结论; .
.