题目内容
在极坐标系中,已知圆 的圆心
的圆心 ,半径
,半径 .
.
(Ⅰ)求圆 的极坐标方程;
的极坐标方程;
(Ⅱ)若 ,直线
,直线 的参数方程为
的参数方程为 (
( 为参数),直线
为参数),直线 交圆
交圆 于
于 两点,求弦长
两点,求弦长 的取值范围.
的取值范围.
 的圆心
的圆心 ,半径
,半径 .
.(Ⅰ)求圆
 的极坐标方程;
的极坐标方程;(Ⅱ)若
 ,直线
,直线 的参数方程为
的参数方程为 (
( 为参数),直线
为参数),直线 交圆
交圆 于
于 两点,求弦长
两点,求弦长 的取值范围.
的取值范围.①. .②.
.②. .
.
 .②.
.②. .
.试题分析:(Ⅰ) 先建立圆的直角坐标方程,再化成极坐标方程,或直接建立极坐标方程. (Ⅱ)直线参数方程中参数的几何意义及应用于求弦长,再运用三角函数求范围.
试题解析:(Ⅰ)【法一】∵
 的直角坐标为
的直角坐标为 ,
,∴圆
 的直角坐标方程为
的直角坐标方程为 .
.化为极坐标方程是
 .
.
【法二】设圆
 上任意一点
上任意一点 ,则
,则如图可得,
 .
. 化简得
 4分
4分(Ⅱ)将
 代入圆
代入圆 的直角坐标方程
的直角坐标方程 ,
,得

即

有
 .
.故
 ,
,∵
 ,
,∴
 ,
,即弦长
 的取值范围是
的取值范围是 10分
10分
练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
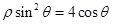 ,直线
,直线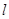 的参数方程为
的参数方程为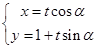 (t为参数,
(t为参数,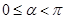 )
) 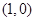 ,求直线
,求直线 中,曲线
中,曲线 的参数方程为
的参数方程为 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点 为极点,
为极点, 轴的正半轴为极轴的极坐标系下,曲线
轴的正半轴为极轴的极坐标系下,曲线 的方程为
的方程为 .
. 、
、 ,求
,求 .
.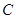 的极坐标方程为
的极坐标方程为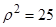 ,曲线
,曲线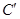 的极坐标方程为
的极坐标方程为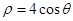 .试求曲线
.试求曲线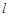 的参数方程为
的参数方程为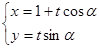 (t为参数,0<a<
(t为参数,0<a<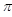 ),曲线C的极坐标方程为
),曲线C的极坐标方程为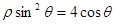 .
. (
( )截圆
)截圆 所得弦长是 .
所得弦长是 . 与
与 的公共点到极点的距离为__________
的公共点到极点的距离为__________ ,以极点为原点,极轴为
,以极点为原点,极轴为 轴正半轴建立直角坐标系,则该曲线的直角坐标方程为
轴正半轴建立直角坐标系,则该曲线的直角坐标方程为  与曲线
与曲线 的交点间距离为
的交点间距离为