题目内容
7．如图，在圆C中，点A、B在圆上，则$\overrightarrow{AB}•\overrightarrow{AC}$的值（ ）
| A． | 只与圆C的半径有关 | |
| B． | 既与圆C的半径有关，又与弦AB的长度有关 | |
| C． | 只与弦AB的长度有关 | |
| D． | 是与圆C的半径和弦AB的长度均无关的定值 |
分析 展开数量积，结合向量在向量方向上投影的概念可得$\overrightarrow{AB}•\overrightarrow{AC}$=$\frac{1}{2}|\overrightarrow{AB}{|}^{2}$．则答案可求．
解答 解：如图，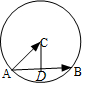
过圆心C作CD⊥AB，垂足为D，则$\overrightarrow{AB}•\overrightarrow{AC}$=|$\overrightarrow{AB}$||$\overrightarrow{AC}$|•cos∠CAB=$\frac{1}{2}|\overrightarrow{AB}{|}^{2}$．
∴$\overrightarrow{AB}•\overrightarrow{AC}$的值只与弦AB的长度有关．
故选：C．
点评 本题考查平面向量的数量积运算，考查向量在向量方向上投影的概念，是中档题．
练习册系列答案
阅读快车系列答案
相关题目
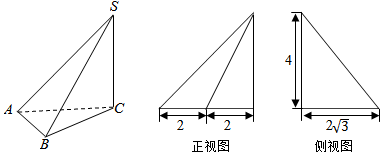
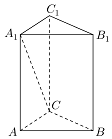如图，已知正三棱柱ABC-A1B1C1的底面积为$\frac{{9\sqrt{3}}}{4}$，侧面积为36；
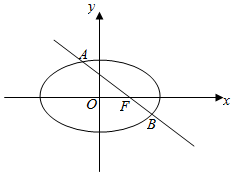椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$过点M（2，0），且右焦点为F（1，0），过F的直线l与椭圆C相交于A、B两点．设点P（4，3），记PA、PB的斜率分别为k1和k2．