题目内容
向量 =(λ,5),
=(λ,5),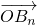 =(n(
=(n( ),0)(n∈N*),
),0)(n∈N*), =(0,m)(m∈N*),
=(0,m)(m∈N*), ,bm=|
,bm=| -
- |2,λ>0.
|2,λ>0.
(1)当λ=1时,求数列{an}的前n项和Sn;
(2)对任意的n,m∈N*,总有 成立,求λ的取值范围.
成立,求λ的取值范围.
解:(1)当λ=1时, .则
.则
又
两式相减得
所以 . …(6分)
. …(6分)
(2) ,
,
∴当m=5时, ,…(8分)
,…(8分)

由 可得n≤2,所以a1<a2=a3>a4>a5>…
可得n≤2,所以a1<a2=a3>a4>a5>…
故有 …(10分)
…(10分)
对任意的n,m∈N*,总有 成立,
成立,
则 ,
,
∴ ,∴
,∴ 或λ>1
或λ>1
因为λ>0,所以λ的取值范围为(1,+∞).…(12分)
分析:(1)确定数列{an}的通项,利用错位相减法,即可求前n项和Sn;
(2)对任意的n,m∈N*,总有 成立,则
成立,则 ,由此可求λ的取值范围.
,由此可求λ的取值范围.
点评:本题考查数列的求和,考查恒成立问题,考查错位相减法,考查学生分析解决问题的能力,属于中档题.
 .则
.则
又

两式相减得

所以
 . …(6分)
. …(6分)(2)
 ,
,∴当m=5时,
 ,…(8分)
,…(8分)
由
 可得n≤2,所以a1<a2=a3>a4>a5>…
可得n≤2,所以a1<a2=a3>a4>a5>…故有
 …(10分)
…(10分)对任意的n,m∈N*,总有
 成立,
成立,则
 ,
,∴
 ,∴
,∴ 或λ>1
或λ>1因为λ>0,所以λ的取值范围为(1,+∞).…(12分)
分析:(1)确定数列{an}的通项,利用错位相减法,即可求前n项和Sn;
(2)对任意的n,m∈N*,总有
 成立,则
成立,则 ,由此可求λ的取值范围.
,由此可求λ的取值范围.点评:本题考查数列的求和,考查恒成立问题,考查错位相减法,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
与向量
=(12,5)平行的单位向量为( )
| a |
A、(
| ||||||||
B、(-
| ||||||||
C、(
| ||||||||
D、(-
|
过点P(-3,1)且方向向量为
=(2,-5)的光线经直线y=-2反射后通过抛物线y2=mx,(m≠0)的焦点,则抛物线的方程为( )
| a |
| A、y2=-2x | ||
B、y2=-
| ||
| C、y2=4x | ||
| D、y2=-4x |