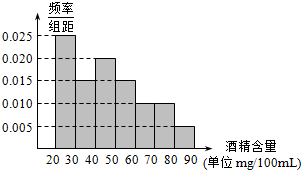
题目内容
3．
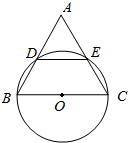如图，以⊙O的直径BC为一边作等边△ABC，AB、AC交⊙O于点DE，求证：BD=DE=EC．
分析 连接OD、OE，构建等边△OBD、△ODE、△OEC；然后由等边三角形的性质和圆心角、弧、弦的关系证得BD=DE=EC．
解答 
证明：如图，连接OD、OE．
∵△ABC是等边三角形，
∴∠B=60°．
又∵OB=OD，
∴△OBD是等边三角形，
∴∠BOD=60°．
同理，△EOC是等边三角形，则∠EOC=60°．
∵BC是⊙O的直径，
∴∠DOE=180°-∠BOD-∠EOC=60°，
∴$\widehat{BD}$=$\widehat{DE}$=$\widehat{EC}$，
∴BD=DE=EC．
点评 本题考查了圆周角定理，等边三角形的性质以及圆周角、弧、弦的关系．解题的难点是辅助线的做法．
练习册系列答案
相关题目
18．已知c≠0，且a，b，c，2b成等差数列，则$\frac{a}{c}$=（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
8．一个几何体的三视图如图所示，则这个几何体的体积为（ ）
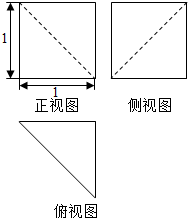
| A． | $\frac{5}{6}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{6}$ |
