题目内容
10.已知集合A={x|1≤x≤4},B={x|x<2或x>4},求:①A∩B
②∁R(A∪B)
分析 根据交集、并集和补集的定义,即可求出对应的结果.
解答 解:①A∩B={x|1≤x≤4}∩{x|x<2或x>4}={x|1≤x<2},
②A∪B={x|1≤x≤4}∪{x|x<2或x>4}=R,
∴∁R(A∪B)=∅.
点评 本题考查了交集、并集和补集的运算与应用问题,是基础题目.

练习册系列答案
相关题目
20.已知e=2.71828…,设函数f(x)=$\frac{1}{2}$x2-bx+alnx存在极大值点x0,且对于b的任意可能取值,恒有极大值f(x0)<0,则下列结论中正确的是( )
| A. | 存在x0=$\sqrt{a}$,使得f(x0)<-$\frac{1}{e}$ | B. | 存在x0=$\sqrt{a}$,使得f(x0)>-e | ||
| C. | a的最大值为e2 | D. | a的最大值为e3 |
18.如图所示的程序框图中的错误是( )
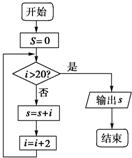

| A. | i没有赋值 | B. | 循环结构有错 | C. | s的计算不对 | D. | 判断条件不成立 |
2.已知定义域为(0,+∞)的函数f(x)满足:(1)对任意x∈(0,+∞),恒有f(2x)=2f(x)成立;(2)当x∈(1,2]时,f(x)=2-x.
给出如下结论:
①对任意m∈Z,有f(2m)=0;
②函数f(x)的值域为[0,+∞);
③存在n∈Z,使得f(2n+1)=9;
正确的有( )
给出如下结论:
①对任意m∈Z,有f(2m)=0;
②函数f(x)的值域为[0,+∞);
③存在n∈Z,使得f(2n+1)=9;
正确的有( )
| A. | ①②③ | B. | ①② | C. | ①③ | D. | ②③ |