Question

求证:两两相交且不共点的四条直线在同一平面内.

Answer 1

思路分析:可先依据两条直线确定一个平面,再证其他两条直线在这个平面内.可分有三点共线和无三点共线两种情况进行证明.

证明:已知a,b,c,d是两两相交且不共点的四条直线,求证:a,b,c,d共面.

(1)无三线共点情况,如图213,设a∩d=M,b∩d=N,c∩d=P,a∩b=Q,a∩c=R,b∩c=S.

∵a∩d=M,∴a,d可确定一个平面α.

∵N∈d,Q∈a,∴N∈α,Q∈α,

∴NQα,即bα.

同理cα.∴a,b,c,d共面.

(2)有三线共点的情况,如图2-1-4,设b,c,d三线相交于点K,与a分别交于N,P,M且Ka.

∵Kα,∴K和a确定一个平面,设为β.

∵N∈a,aβ,∴N∈β.

∴NKβ即bβ.

同理cβ,dβ,∴a,b,c,d共面.

由(1)(2)知a,b,c,d共面.

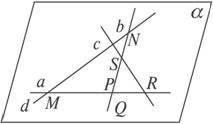
图2-1-3

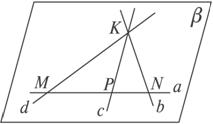
图2-1-4