题目内容
(本小题共14分)
已知椭圆![]() (a>b>0)的离心率
(a>b>0)的离心率![]() ,椭圆上任意一点到椭圆的两个焦点的距离之和为4.设直线l与椭圆相交于不同的两点A、B,点A的坐标为(
,椭圆上任意一点到椭圆的两个焦点的距离之和为4.设直线l与椭圆相交于不同的两点A、B,点A的坐标为(![]() ,0).
,0).
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若![]() ,求直线l的倾斜角;
,求直线l的倾斜角;
(Ⅲ)若点Q![]() 在线段AB的垂直平分线上,且
在线段AB的垂直平分线上,且![]() ,求
,求![]() 的值.
的值.
(本小题共14分)
解:(I)由题意可知![]() ,e
,e![]()
![]() ,得
,得![]() ,
,![]() ,解得
,解得![]() . -2分
. -2分
所以椭圆的方程为![]() . --3分
. --3分
(Ⅱ)由(I)可知点A的坐标是(![]() 2,0).设点B的坐标为
2,0).设点B的坐标为![]() ,直线l的斜率为k,则直线l
,直线l的斜率为k,则直线l
的方程为![]() .
.
于是A、B两点的坐标满足方程组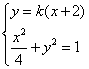 --4分
--4分
消去y并整理,得![]() . ------5分
. ------5分
由![]() ,得
,得![]() ,从而
,从而![]() .
.
所以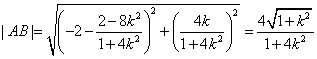 . ------6分
. ------6分
由![]() ,得
,得![]() .
.
整理得![]() ,即
,即![]() ,解得k=
,解得k=![]() .-------7分
.-------7分
所以直线l的倾斜角为![]() 或
或![]() . -- 8分
. -- 8分
(Ⅲ)设线段AB的中点为M,由(II)得到M的坐标为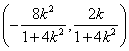 .以下分两种情况:
.以下分两种情况:
(1) 当k![]() 0时,点B的坐标是(2,0),线段AB的垂直平分线为y轴,于是
0时,点B的坐标是(2,0),线段AB的垂直平分线为y轴,于是
![]() ,由
,由![]() ,得
,得![]() .------10分
.------10分
(2)当![]() 时,线段AB的垂直平分线方程为
时,线段AB的垂直平分线方程为
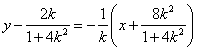
令![]() ,解得
,解得![]() . --11分
. --11分
由![]() ,
,![]() ,
,
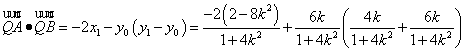
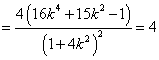 , --12分
, --12分
整理得![]() ,故
,故![]() ,所以
,所以![]() . ----13分
. ----13分
综上,![]() 或
或![]() ----14分
----14分

练习册系列答案
相关题目

 底面ABCD,PD=DC,点E是PC的中点,作EF
底面ABCD,PD=DC,点E是PC的中点,作EF
 的棱长为
的棱长为 ,
, 是
是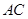 与
与 的交点,
的交点, 为
为 的中点.
的中点. ∥平面
∥平面 ;
; 平面
平面 ;
; 的体积.
的体积.