题目内容
如图所示,在△ABC中,点M是BC的中点,点N在AC上,且AN=2NC,AM与BN相交于点P,求AP∶PM的值.

AP∶PM=4∶1
解析:
方法一 设e1=![]() ,e2=
,e2=![]() ,
,
则![]() =
=![]() +
+![]() =-3e2-e1,
=-3e2-e1,
![]() =
=![]() +
+![]() =2e1+e2.
=2e1+e2.
因为A、P、M和B、P、N分别共线,所以存在实数![]() 、
、![]() ,使
,使![]() =
=![]()
![]() =-3
=-3![]() e2-
e2-![]() e1,
e1,
![]() =
=![]()
![]() =2
=2![]() e1+
e1+![]() e2,∴
e2,∴![]() =
=![]() -
-![]() =(
=(![]() +2
+2![]() )e1+(3
)e1+(3![]() +
+![]() )e2,
)e2,
另外![]() =
=![]() +
+![]() =2e1+3e2,
=2e1+3e2,
![]() ,∴
,∴![]() ,
,
∴![]() =
=![]()
![]() ,
,![]() =
=![]()
![]() ,∴AP∶PM=4∶1.
,∴AP∶PM=4∶1.
方法二 设![]() =
=![]()
![]() ,
,
∵![]() =
=![]() (
(![]() +
+![]() )=
)=![]()
![]() +
+![]()
![]() ,
,
∴![]() =
=![]()
![]() +
+![]()
![]()
![]() .
.
∵B、P、N三点共线,∴![]() -
-![]() =t(
=t(![]() -
-![]() ),
),
∴![]() =(1+t)
=(1+t)![]() -t
-t![]()
∴
∴![]() +
+![]()
![]() =1,
=1,![]() =
=![]() ,∴AP∶PM=4∶1.
,∴AP∶PM=4∶1.

练习册系列答案
相关题目
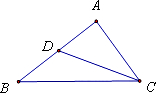 如图所示,在△ABC中,点D是边AB的中点,则向量
如图所示,在△ABC中,点D是边AB的中点,则向量| DC |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
 如图所示,在△ABC,已知
如图所示,在△ABC,已知 如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=
如图所示,在△ABC中,∠B=60°,∠C=45°,高AD= 如图所示,在△ABC中,∠BAC=90°,∠ABC=60°,AD⊥BC于D,则
如图所示,在△ABC中,∠BAC=90°,∠ABC=60°,AD⊥BC于D,则 如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=
如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=