题目内容
【题目】
， 
为两个定点， 
是 
的一条切线，若过 
两点的抛物线以直线 为准线，则该抛物线的焦点的轨迹方程是 ．
【答案】
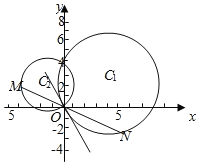
【解析】根据题意画出图像，任意画出一条切线，作AB垂直于切线于CD两点，设抛物线的焦点为F点，根据抛物线的定义得到 
， 
，因为O为AB的中点，作OG垂直于切线于点G，OG为梯形ABCE的中位线，故得到|BF|+|AF|=2|OG|=8，故根据椭圆的定义得到轨迹是以AB为焦点的椭圆长半轴为4，c=2,故得到轨迹方程为 ，由条件知焦点一定不能落在x轴上故需要去掉两点。
所以答案是： 。
【考点精析】利用椭圆的概念和椭圆的标准方程对题目进行判断即可得到答案，需要熟知平面内与两个定点
，
的距离之和等于常数（大于
）的点的轨迹称为椭圆,这两个定点称为椭圆的焦点，两焦点的距离称为椭圆的焦距；椭圆标准方程焦点在x轴：
，焦点在y轴：
．
练习册系列答案
相关题目
