题目内容
 如图所示是长方体截去一个角后得到的几何体,其中底面ABCD是边长为2
如图所示是长方体截去一个角后得到的几何体,其中底面ABCD是边长为2| 3 |
(1)求四棱锥E-ABCD的体积;
(2)正方形ABCD内(包括边界)是否存在点M,使三棱锥H-AMB体积是四棱锥E-ABCD体积的
| 1 |
| 8 |
考点:棱柱、棱锥、棱台的体积,轨迹方程
专题:综合题,空间位置关系与距离
分析:(1)利用四棱锥体积公式,可得四棱锥E-ABCD的体积;
(2)先求出M到平面AHB的距离,再确定点M的轨迹.
(2)先求出M到平面AHB的距离,再确定点M的轨迹.
解答:
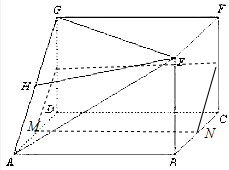 解:(1)由题意,四棱锥E-ABCD的体积为
解:(1)由题意,四棱锥E-ABCD的体积为
×2
×2
×2=8;
(2)∵H为AG中点,∴S△AHB=
×2
×2=2
,
设M到平面AHB的距离为h,则
∵三棱锥H-AMB体积是四棱锥E-ABCD体积的
,
∴
×2
h=
×4,
∴h=
,
∴M到平面AHB的距离为
,
在AD上取点M,使得AM=
,在平面ABCD内作MN∥AB,交BC于N,则MN为所求轨迹.
 解:(1)由题意,四棱锥E-ABCD的体积为
解:(1)由题意,四棱锥E-ABCD的体积为| 1 |
| 3 |
| 3 |
| 3 |
(2)∵H为AG中点,∴S△AHB=
| 1 |
| 2 |
| 3 |
| 3 |
设M到平面AHB的距离为h,则
∵三棱锥H-AMB体积是四棱锥E-ABCD体积的
| 1 |
| 8 |
∴
| 1 |
| 3 |
| 3 |
| 1 |
| 8 |
∴h=
| ||
| 4 |
∴M到平面AHB的距离为
| ||
| 4 |
在AD上取点M,使得AM=
| ||
| 2 |
点评:本题考查棱柱、棱锥、棱台的体积,考查轨迹方程,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
已知α为第二象限角,sinα=
,则sin(2α+π)=( )
| 3 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
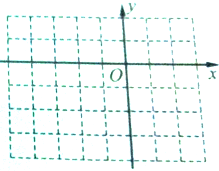 写出下列向量的坐标表示,并在如图所示的正方形网格图中作出下列向量(以O为起点).
写出下列向量的坐标表示,并在如图所示的正方形网格图中作出下列向量(以O为起点). 如图,已知A是△BCD所在平面外一点,M是平面ABC上的一点,试过D、M两点作一平面,使这个平面平行于BC,并说明理由.
如图,已知A是△BCD所在平面外一点,M是平面ABC上的一点,试过D、M两点作一平面,使这个平面平行于BC,并说明理由.