题目内容
20.不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{y≤-kx+4k}\end{array}\right.$(k>0)所表示平面区域的面积为S,则$\frac{{k}^{2}+1}{S}$的最小值等于( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
分析 先画出不等式组所表示的平面区域,然后用k表示出图形的面积,进而表示出$\frac{{k}^{2}+1}{S}$,最后利用基本不等式求出它的最值即可
解答 解:不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{y≤-kx+4k}\end{array}\right.$(k>0)所表示平面区域如图,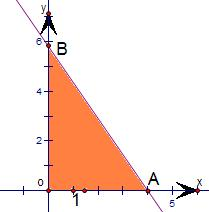
A(4,0),B(0,4k),
根据题意可知三角形OAB为直角三角形,其面积等于
$\frac{1}{2}$×|OA|×|OB|=8k,
∴$\frac{{k}^{2}+1}{S}$=$\frac{{k}^{2}+1}{8k}=\frac{1}{8}(k+\frac{1}{k})≥\frac{1}{8}×2\sqrt{k•\frac{1}{k}}=\frac{1}{4}$,(k>0)
当且仅当k=1时等号,
∴$\frac{{k}^{2}+1}{S}$的最小值为$\frac{1}{4}$,
故选C.
点评 本题考查简单的线性规划,以及利用基本不等式等知识求最值问题,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知函数f(x)=$\left\{\begin{array}{l}{{3}^{x},x≥0}\\{lo{g}_{3}(-x),x<0}\end{array}\right.$,函数g(x)=f2(x)+f(x)+t(t∈R).关于函数g(x)的零点,下列判断不正确的是( )
| A. | 若t<-2,g(x)有四个零点 | B. | 若t=-2,g(x)有三个零点 | ||
| C. | 若-2<t<$\frac{1}{4}$,g(x)有两个零点 | D. | 若t=$\frac{1}{4}$,g(x)有一个零点 |
8.已知等比数列{an}的前n项和为Sn,且4a1,2a2,a3依次等差数列,若a1=1,则S5=( )
| A. | 16 | B. | 31 | C. | 32 | D. | 63 |
12.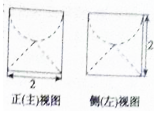 若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图所示,则此几何体的表面积是( )
若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图所示,则此几何体的表面积是( )
 若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图所示,则此几何体的表面积是( )
若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图所示,则此几何体的表面积是( )| A. | (4+$\sqrt{2}$)π | B. | 6$π+2\sqrt{2}π$ | C. | 6$π+\sqrt{2}π$ | D. | (8+$\sqrt{2}$)π |