题目内容
12分)已知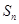 是数列
是数列 的前
的前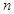 项和,且对任意
项和,且对任意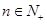 ,有
,有 .记
.记 .其中
.其中 为实数,且
为实数,且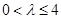 .
.
(1)当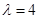 时,求数列
时,求数列 的通项;
的通项;
(2)当 时,若
时,若 对任意
对任意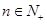 恒成立,求
恒成立,求 的取值范围.
的取值范围.
【答案】
 时,
时,  ∴
∴
 时
时 相减 ∴
相减 ∴ .
.
则: ∴
∴
(1) 时,
时,  ∴
∴
(2)由
∴
则:
1°当 时,
时, ,
,
 ,
,
∴ 递增,而
递增,而 ∴
∴ 只需
只需 , ∴
, ∴
2°当 时,
时, 符合条件
符合条件
3°当 时,
时, ,
,
∴ 递减.
递减.  成立.
成立.
综上所述 .
.
【解析】略

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 是等比数列
是等比数列 的前
的前 项和,且
项和,且 .
. ;
; 是单调递减数列,求实数
是单调递减数列,求实数 的取值范围.
的取值范围. 是等比数列
是等比数列 的公比
的公比 且
且 项的和。若
项的和。若 。(1)求数列
。(1)求数列 ,求数列
,求数列 的前
的前 。
。 是递增的等差数列,满足
是递增的等差数列,满足
 对
对 均有
均有 …+
…+ 成立,求数列
成立,求数列 是数列
是数列 其前
其前 项和,且
项和,且 ,
, .
. ,且
,且 是数列
是数列 的前
的前 对所有
对所有 都成立的最小正整数
都成立的最小正整数 .
.