题目内容

3．已知tanα=2，则$\frac{2sinα-cosα}{sinα+cosα}$=1．

分析 化简所求的表达式为正切函数的形式，代入求解即可．

解答 解：tanα=2，则$\frac{2sinα-cosα}{sinα+cosα}$=$\frac{2tanα-1}{tanα+1}$=$\frac{4-1}{2+1}$=1．
故答案为：1．

点评 本题考查三角函数的化简求值，考查计算能力．

练习册系列答案
相关题目
13．若$|\overrightarrow a|=|\overrightarrow b|=1$，$|3\overrightarrow a-2\overrightarrow b|=3$，则$|3\overrightarrow a+\overrightarrow b|$=2$\sqrt{3}$．
14．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$及实数t满足|$\overrightarrow{a}$+t$\overrightarrow{b}$|=3．若$\overrightarrow{a}$•$\overrightarrow{b}$=2，则t的最大值是$\frac{9}{8}$．
11．若cosα=-$\frac{{\sqrt{3}}}{3}$，sin2α＞0，则tanα的值为（　　）
A．-$\frac{{\sqrt{2}}}{2}$B．$\frac{{\sqrt{2}}}{2}$C．-$\sqrt{2}$D．$\sqrt{2}$
18．已知数列{an}中，a1=1，Sn是数列{an}的前n项和，对任意n≥2，均有3Sn-4、an、2-$\frac{3{S}_{n-1}-1}{2}$成等差数列，则数列{an}的通项公式an=$\left\{\begin{array}{l}{1，n=1}\\{0，n≥2}\end{array}\right.$．
8．化简求值：
（1）sin（$\frac{π}{4}$-3x）cos（$\frac{π}{3}$-3x）-sin（$\frac{π}{4}$+3x）sin（$\frac{π}{3}$-3x）；
（2）sin（α+β）cosα-cos（α+β）sinα；
（3）$\frac{sin27°+cos45°sin18°}{cos27°-sin45°sin18°}$．
15．已知函数f（x）=$\left\{\begin{array}{l}{aln（x+1），x≥0}\\{\frac{1}{3}{x}^{3}-ax，x＜0}\end{array}\right.$，g（x）=ex-1（e为自然对数的底数）
（1）当a＞0时，求函数f（x）的极值；
（2）当a在R上变化时，讨论函数h（x）=g（x）-f（x）的零点的个数；
（3）求证：$\frac{1095}{1000}$＜$\root{10}{e}$＜$\frac{3000}{2699}$．（参考数据：ln1.1≈0.0953）
12．已知△ABC是等腰三角形，则向量$\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$所在的直线与BC垂直（填：平行，垂直）
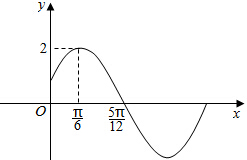13．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示．
（1）求函数f（x）的解析式；
（2）当x∈[-$\frac{π}{6}$，$\frac{5π}{6}$]时，求函数f（x）的单调递增区间；
（3）若关于x的方程f（x）+log2k=0（k为实数）在x∈[$\frac{π}{3}$，$\frac{19π}{24}$]上恒有实数解，求k的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网