题目内容
(本小题满分14分)
在数列 和
和 中,已知
中,已知 ,其中
,其中 且
且 。
。
(I)若 ,求数列
,求数列 的前n项和;
的前n项和;
(II)证明:当 时,数列
时,数列 中的任意三项都不能构成等比数列;
中的任意三项都不能构成等比数列;
(III)设集合 ,试问在区间[1,a]上是否存在实数b使得
,试问在区间[1,a]上是否存在实数b使得 ,若存在,求出b的一切可能的取值及相应的集合C;若不存在,说明理由。
,若存在,求出b的一切可能的取值及相应的集合C;若不存在,说明理由。
在数列
 和
和 中,已知
中,已知 ,其中
,其中 且
且 。
。(I)若
 ,求数列
,求数列 的前n项和;
的前n项和;(II)证明:当
 时,数列
时,数列 中的任意三项都不能构成等比数列;
中的任意三项都不能构成等比数列;(III)设集合
 ,试问在区间[1,a]上是否存在实数b使得
,试问在区间[1,a]上是否存在实数b使得 ,若存在,求出b的一切可能的取值及相应的集合C;若不存在,说明理由。
,若存在,求出b的一切可能的取值及相应的集合C;若不存在,说明理由。(1) (2)略(3)b=1
(2)略(3)b=1
 (2)略(3)b=1
(2)略(3)b=1(I)因为 …………1分
…………1分
由
所以 …………3分
…………3分
因为 …………4分
…………4分
所以 是等差数列, …………4分
是等差数列, …………4分
所以数列 …………5分
…………5分
(II)由已知
假设 成等比数列,其中
成等比数列,其中 ,且彼此不等,
,且彼此不等,
则 …………6分
…………6分

可得 矛盾。 …………7分
矛盾。 …………7分
 为无理数,
为无理数,
所以 是整数矛盾。 …………9分
是整数矛盾。 …………9分
所以数列 中的任意三项都不能构成等比数列。
中的任意三项都不能构成等比数列。
(III)设存在实数 ,
,

所以 整除。 …………10分
整除。 …………10分
(1)当
所以 …………11分
…………11分
(2)当 ,
,

所以,当且仅 当
当 整除。 …………12分
整除。 …………12分
(3)当 时,
时,

 整除。 …………13分
整除。 …………13分
综上,在区间[1,a]上存在实数b,使 成立,且当b=1时,
成立,且当b=1时,

…………14分
 …………1分
…………1分由

所以
 …………3分
…………3分因为
 …………4分
…………4分所以
 是等差数列, …………4分
是等差数列, …………4分所以数列
 …………5分
…………5分(II)由已知

假设
 成等比数列,其中
成等比数列,其中 ,且彼此不等,
,且彼此不等,则
 …………6分
…………6分
可得
 矛盾。 …………7分
矛盾。 …………7分 为无理数,
为无理数,所以
 是整数矛盾。 …………9分
是整数矛盾。 …………9分
所以数列
 中的任意三项都不能构成等比数列。
中的任意三项都不能构成等比数列。(III)设存在实数
 ,
,
所以
 整除。 …………10分
整除。 …………10分(1)当

所以
 …………11分
…………11分(2)当
 ,
,
所以,当且仅
 当
当 整除。 …………12分
整除。 …………12分(3)当
 时,
时,
 整除。 …………13分
整除。 …………13分综上,在区间[1,a]上存在实数b,使
 成立,且当b=1时,
成立,且当b=1时,
…………14分

练习册系列答案
相关题目
 满足:
满足: ,且
,且
 .
. 的值;
的值; ;
; ,求证:
,求证: .
. 为等差数列,
为等差数列, ,
, 以
以 表示
表示 项和,则使得
项和,则使得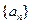 的前
的前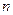 项和为
项和为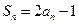 ,数列
,数列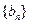 满足
满足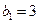 ,
,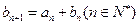 .
.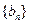 的通项公式; (2)求数列
的通项公式; (2)求数列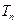 ;
;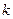 ,使得数列
,使得数列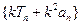 为等差数列,证明你的结论.
为等差数列,证明你的结论.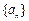 的首项为
的首项为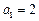 ,前
,前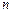 项和为
项和为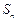 ,且对任意的
,且对任意的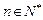 ,
,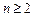 时,
时,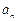 总是
总是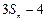 与
与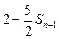 的等差中项.
的等差中项.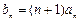 ,
,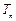 是数列
是数列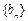 的前
的前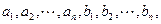 其中
其中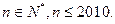
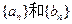 的通项公式;
的通项公式;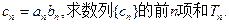
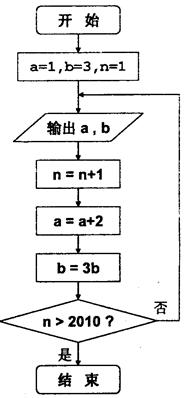
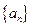 的前n项和为
的前n项和为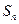 ,若
,若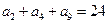 ,则
,则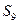 = ;
= ;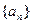 的前n项和为
的前n项和为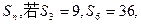 则
则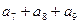 =" " ( )
=" " ( )