题目内容
如图，空间四边形ABCD中，AB、BC、CD的中点分别是P、Q、R，且
，那么异面直线BD和PR所成的角是
- A.90度
- B.60度
- C.45度
- D.30度
B
分析：先利用三角形中位线定理证明QR∥BD，从而∠PRQ就是异面直线BD和PR所成的角，再在三角形PQR中利用解直角三角形知识计算此角即可
解答：∵空间四边形ABCD中，AB、BC、CD的中点分别是P、Q、R，
∴QR∥BD
∴∠PRQ就是异面直线BD和PR所成的角
在三角形PQR中，
∴PQ2+QR2=PR2
∴∠PQR=90°，又tan∠PRQ=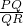
=
∴∠PRQ=60°
∴异面直线BD和PR所成的角是60°
故选 B
点评：本题考查了空间异面直线所成的角的作法、证法、求法，将空间角问题转化为求平面角问题是解决本题的关键
分析：先利用三角形中位线定理证明QR∥BD，从而∠PRQ就是异面直线BD和PR所成的角，再在三角形PQR中利用解直角三角形知识计算此角即可
解答：∵空间四边形ABCD中，AB、BC、CD的中点分别是P、Q、R，
∴QR∥BD
∴∠PRQ就是异面直线BD和PR所成的角
在三角形PQR中，
∴PQ2+QR2=PR2
∴∠PQR=90°，又tan∠PRQ=
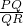=∴∠PRQ=60°
∴异面直线BD和PR所成的角是60°
故选 B
点评：本题考查了空间异面直线所成的角的作法、证法、求法，将空间角问题转化为求平面角问题是解决本题的关键
练习册系列答案
相关题目
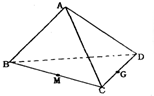如图，空间四边形ABCD中，M、G分别是BC、CD的中点，则| AB |
| 1 |
| 2 |
| BC |
| 1 |
| 2 |
| BD |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，空间四边形ABCD的对棱AD、BC成60°的角，且AD=BC=4，平行于AD与BC的截面分别交AB、AC、CD、BD于E、F、G、H．
如图，空间四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA的中点．
如图，空间四边形ABCD中，AB、BC、CD的中点分别是P、Q、R，且
如图，空间四边形ABCD中，E、F分别是AB、AD的中点，G、H分别在BC、CD上，且BG：GC=DH：HC=1：2