题目内容
5.一个半径为r的扇形,若它的周长等于它所在圆的周长的一半,则扇形所对圆心角的度数为(π-2)rad.分析 设圆心角为θ,半径为r,弧长为l,建立方程,求得弧长与半径的关系,再求扇形的圆心角即可.
解答 解:设圆心角为θ,半径为r,弧长为l,
由题意得2r+l=πr,解得l=(π-2)r,
可得:圆心角θ=$\frac{l}{r}$=π-2.
故答案为:(π-2)rad.
点评 本题考查弧长公式,解题的关键是熟练掌握弧长公式,属基础题.

练习册系列答案
相关题目
13.函数$y=\sqrt{2x+1}+ln(3-4x)$的定义域为( )
| A. | $(-\frac{1}{2},\frac{3}{4})$ | B. | $[-\frac{1}{2},\frac{3}{4}]$ | C. | $(-∞,\frac{1}{2}]∪(\frac{3}{4},+∞)$ | D. | $[-\frac{1}{2},\frac{3}{4})$ |
10.已知$|{\overrightarrow{a}}|=4,\;|{\overrightarrow{b}}|=5$,且$\overrightarrow{a}⊥\overrightarrow{b}$,则$\overrightarrow{a}•\overrightarrow{b}$=( )
| A. | 0 | B. | 10 | C. | 20 | D. | -20 |
17.已知$\overrightarrow{a}$、$\overrightarrow{b}$为单位向量,|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{2}$|$\overrightarrow{a}-\overrightarrow{b}$|,则$\overrightarrow{a}$在$\overrightarrow{a}+\overrightarrow{b}$的投影为( )
| A. | $\frac{1}{3}$ | B. | -$\frac{2\sqrt{6}}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
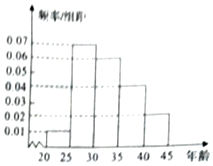 某地为增强居民的传统文化意识,活跃节日氛围,在元宵节举办了猜灯谜比赛,现从参加比赛的选手中随机抽取200名后按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45),得到的频率分布直方图如图所示.
某地为增强居民的传统文化意识,活跃节日氛围,在元宵节举办了猜灯谜比赛,现从参加比赛的选手中随机抽取200名后按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45),得到的频率分布直方图如图所示. 如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.