题目内容
(本小题满分14分)已知函数
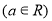
(1)求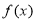 的单调区间和极值;
的单调区间和极值;
(2)设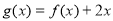 ,若
,若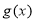 在
在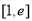 上不单调且仅在
上不单调且仅在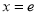 处取得最大值,求
处取得最大值,求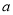 的取值范围;
的取值范围;
(3)当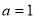 时,探究当
时,探究当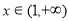 时,函数
时,函数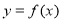 的图像与函数
的图像与函数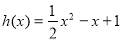 图像之间的关系,并证明你的结论.
图像之间的关系,并证明你的结论.
(1)当a≤0时, 在(0,+∞)上单调递增,无极值;当a>0时,函数
在(0,+∞)上单调递增,无极值;当a>0时,函数 的增区间为
的增区间为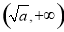 ,减区间为
,减区间为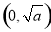 ,在
,在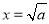 取得极小值,极小值为
取得极小值,极小值为 ;(2)a∈
;(2)a∈ ;(3)略.
;(3)略.
【解析】
试题分析:(1)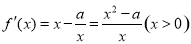 ,若a≤0,则
,若a≤0,则 ,
, 在(0,+∞)上单调递增;
在(0,+∞)上单调递增;
若a>0,则由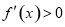 解得
解得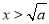 ;由
;由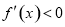 解得
解得 ,
,
此时函数的增区间为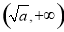 ,减区间为
,减区间为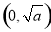 .
.
当a>0时,则在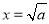 取得极小值,极小值为
取得极小值,极小值为 ;
;
当a≤0时时,无极值.
(2)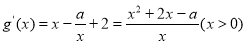 ,
,
设
 ,
,
若 在
在 上不单调,则
上不单调,则 ,∴
,∴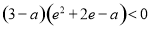 ,∴
,∴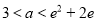 ,
,
同时 仅在
仅在 处取得最大值,
处取得最大值,
∴只要g(e)>g(1)即可得出: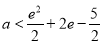 ,
,
故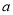 的范围:
的范围:
(3)结论:在区间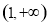 上,函数
上,函数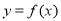 的图像总在函数
的图像总在函数 图像的上方.
图像的上方.
即证当x>1时,f(x)>h(x),即lnx+1<x.
设m(x)=lnx+1-x,则 ,
,
有m(x)在(1,+ ∞)上单调递减,∴m(x)<m(1),得证.
考点:考查了利用导数研究函数的单调性和极值,证明不等式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的解集是 ( )
的解集是 ( ) B.
B. C.
C. D.
D.
 α D.b∥α或b
α D.b∥α或b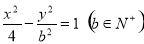 的两个焦点为
的两个焦点为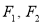 ,
,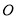 为坐标原点,点
为坐标原点,点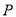 在双曲线上,且
在双曲线上,且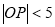 ,若
,若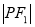 、
、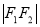 、
、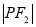 成等比数列,则
成等比数列,则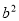 等于( )
等于( )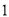 B.
B.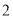 C.
C. D.
D.
 ( )
( )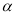 的终边在第二象限,且与单位圆交于点
的终边在第二象限,且与单位圆交于点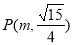 .
.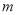 的值;
的值; 的值.
的值.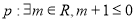 ,命题
,命题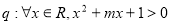 .若“
.若“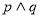 ”为假命题,则实数
”为假命题,则实数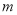 的取值范围是( )
的取值范围是( )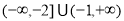 B.
B.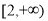
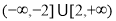 D.
D.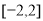
 恒成立,则实数m的最大值为 .
恒成立,则实数m的最大值为 . 的值域
的值域