题目内容
如图,椭圆的中心为原点O,已知右准线l的方程为x=4,右焦点F到它的距离为2.
(1)求椭圆的标准方程;
(2)设圆C经过点F,且被直线l截得的弦长为4,求使OC长最小时圆C的方程.
 |
解:(1)设椭圆的标准方程为![]() +
+![]() =1(a>b>0).
=1(a>b>0).
由题意可得![]() ,………………………………………………………………………2分
,………………………………………………………………………2分
解得a=2![]() ,c=2.…………………………………………………………………………4分
,c=2.…………………………………………………………………………4分
从而b2=a2-c2=4.
所以椭圆的标准方程为![]() +
+![]() =1.……………………………………………………………6分
=1.……………………………………………………………6分
(2)设圆C的方程为(x-m)2+(y-n)2=r2,r>0.
由圆C经过点F(2,0),得(2-m)2+n2=r2, ①……………………………7分
由圆C被l截得的弦长为4,得|4-m|2+(![]() )2=r2, ②……………………………8分
)2=r2, ②……………………………8分
联立①②,消去r得:n2=16-4m.………………………………………………………10分
所以OC=![]() =
=![]() =
=![]() .……………………………………12分
.……………………………………12分
因为由n2≥0可得m≤4,
所以当m=2时,OC长有最小值2![]() .……………………………………………………14分
.……………………………………………………14分
此时n=±2![]() ,r=2
,r=2![]() ,故所求圆C的方程为(x-2)2+(y±2
,故所求圆C的方程为(x-2)2+(y±2![]() )2=8.………………16分
)2=8.………………16分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
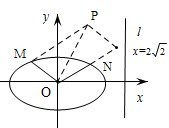 如图,椭圆的中心为原点O,离心率e=
如图,椭圆的中心为原点O,离心率e=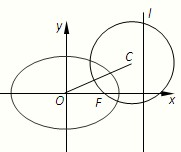 如图,椭圆的中心为原点O,已知右准线l的方程为x=4,右焦点F到它的距离为2.
如图,椭圆的中心为原点O,已知右准线l的方程为x=4,右焦点F到它的距离为2. (2013•重庆)如图,椭圆的中心为原点O,长轴在x轴上,离心率
(2013•重庆)如图,椭圆的中心为原点O,长轴在x轴上,离心率 (2013•重庆)如图,椭圆的中心为原点O,长轴在x轴上,离心率
(2013•重庆)如图,椭圆的中心为原点O,长轴在x轴上,离心率
 ,线段
,线段 的中点分别为
的中点分别为 ,且△
,且△ 是面积为4的直角三角形.
是面积为4的直角三角形. 做直线
做直线 交椭圆于P,Q两点,使
交椭圆于P,Q两点,使 ,求直线
,求直线