题目内容
【题目】已知函数![]() ,
, ![]() ,(
,( ![]() 为常数)
为常数)
(1)若![]() 在
在![]() 处的切线方程为
处的切线方程为![]() (
(![]() 为常数),求
为常数),求![]() 的值;
的值;
(2)设函数![]() 的导函数为
的导函数为![]() ,若存在唯一的实数
,若存在唯一的实数![]() ,使得
,使得![]() 与
与![]() 同时成立,求实数
同时成立,求实数![]() 的取值范围;
的取值范围;
(3)令![]() ,若函数
,若函数![]() 存在极值,且所有极值之和大于
存在极值,且所有极值之和大于![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)求函数的导数,利用导数的几何意义,建立条件关系即可求出b的值.
(2)求函数的导数,解f(x0)=x0与f′(x0)=0,即可得到结论.
(3)求出F(x)的导数,根据函数极值和导数之间的关系,即可得到结论.
试题解析:
(1)∵![]() 所以直线
所以直线![]() 的
的![]() ,
,
当![]() 时,
时, ![]() ,将
,将![]() 代入
代入![]() ,得
,得![]() .
.
(2)![]() ,由题意知
,由题意知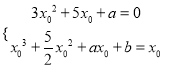 消去
消去![]() ,
,
得![]() 有唯一解.
有唯一解.
令![]() ,则
,则![]() ,
,
所以![]() 在区间
在区间![]() ,区间
,区间![]() 上是增函数,在
上是增函数,在![]() 上是减函数,
上是减函数,
又![]() ,故实数
,故实数![]() 的取值范围是
的取值范围是![]() .
.
(3)![]() ,∴
,∴![]()
因为![]() 存在极值,所以
存在极值,所以![]() 在
在![]() 上有根即方程
上有根即方程![]() 在
在![]() 上有根.
上有根.
记方程![]() 的两根为
的两根为![]() 由韦达定理
由韦达定理 ,所以方程的根必为两不等正跟.
,所以方程的根必为两不等正跟.
![]()
![]()
所以![]() 满足方程
满足方程![]() 判别式大于零
判别式大于零
故所求取值范围为![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】媒体为调查喜欢娱乐节目![]() 是否与性格外向有关,随机抽取了400名性格外向的和400名性格内向的居民,抽查结果用等高条形图表示如下图:
是否与性格外向有关,随机抽取了400名性格外向的和400名性格内向的居民,抽查结果用等高条形图表示如下图:
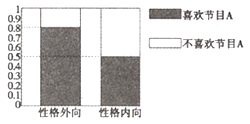
(1)填写完整如下![]() 列联表;
列联表;

(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.001的前提下认为喜欢娱乐节目![]() 与性格外向有关?
与性格外向有关?
参考数据及公式:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
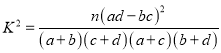
【题目】为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议.现对他前![]() 次考试的数学成绩
次考试的数学成绩![]() 、物理成绩进行分析.下面是该生
、物理成绩进行分析.下面是该生![]() 次考试的成绩.
次考试的成绩.
数学 | 108 | 103 | 137 | 112 | 128 | 120 | 132 |
物理 | 74 | 71 | 88 | 76 | 84 | 81 | 86 |
(Ⅰ)他的数学成绩与物理成绩哪个更稳定?请给出你的说明;
(Ⅱ)已知该生的物理成绩![]() 与数学成绩是线性相关的,求物理成绩
与数学成绩是线性相关的,求物理成绩![]() 与数学成绩的回归直线方程
与数学成绩的回归直线方程
(Ⅲ)若该生的物理成绩达到90分,请你估计他的数学成绩大约是多少?
(附: 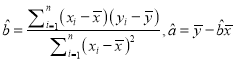 )
)