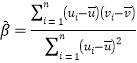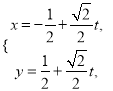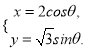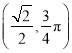[题目]某小组共10人.利用假期参加义工活动.已知参加义工活动1次的有2人.2次的有4人.3次的有4人.现从这10人中随机选出2人作为该组代表参加座谈会.(1)设为事件“选出的2人参加义工活动次数之和为4 .求事件发生的概率,(2)设为选出的2人参加义工活动次数之差的绝对值.求随机变量的分布列和数学期望. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】某小组共10人，利用假期参加义工活动，已知参加义工活动1次的有2人，2次的有4人，3次的有4人.现从这10人中随机选出2人作为该组代表参加座谈会.

（1）设为事件“选出的2人参加义工活动次数之和为4”，求事件发生的概率；

（2）设为选出的2人参加义工活动次数之差的绝对值，求随机变量的分布列和数学期望.

【答案】（1）.（2）见解析.

【解析】试题分析：（1）由已知得，即可得到事件的概率.

（2）由题意得，得到随机变量的所有可能取值，求得随机变量取每个值的概率，即可得到随机变量的分布列，并计算其数学期望.

试题解析：

（1）由已知得.所以事件发生的概率为.

（2）随机变量的所有可能取值为0，1，2

计算，

，

；

所以随机变量的分布列为：

随机变量的数学期望为.

练习册系列答案

相关题目

【题目】已知、、是函数的三个极值点,且,有下列四个关于函数的结论:①；②；③；④恒成立,其中正确的序号为__________．

【题目】某中学从参加高一年级上学期期末考试的学生中抽出60名学生，将其成绩(均为整数)分成六段[40，50)，[50，60)，…，[90，100]后画出如下部分频率分布直方图.观察图形的信息，回答下列问题：

(1)估计这次考试的及格率(60分及以上为及格).

(2)从成绩是70分以上(包括70分)的学生中选一人，求选到第一名学生的概率(第一名学生只一人).

【题目】菜农定期使用低害杀虫农药对蔬菜进行喷洒，以防止害虫的危害，但采集上市时蔬菜仍存有少量的残留农药，食用时需要用清水清洗干净，下表是用清水（单位：千克）清洗该蔬菜1千克后，蔬菜上残留的农药（单位：微克）的统计表：

（1）令，利用给出的参考数据求出关于的回归方程.（，精确到0.1）

参考数据：，，

其中，

（2）对于某种残留在蔬菜上的农药，当它的残留量不高于20微克时对人体无害，为了放心食用该蔬菜，请估计至少需用用多少千克的清水清洗1千克蔬菜？（精确到0.1，参考数据）

附：对于一组数据，，…，，其回归直线的斜率和截距的最小二乘估计分别为

，.

【题目】选修4-4：坐标系与参数方程

已知直线的参数方程为椭圆的参数方程为在以坐标原点为极点，轴正半轴为极轴建立的极坐标系中，点的坐标为.

（1）将点的坐标化为直角坐标系下的坐标，椭圆的参数方程化为普通方程；

（2）直线与椭圆交于，两点，求的值.

【题目】已知函数，，（为常数）

（1）若在处的切线方程为（为常数），求的值；

（2）设函数的导函数为，若存在唯一的实数，使得与同时成立，求实数的取值范围；

（3）令，若函数存在极值，且所有极值之和大于，求的取值范围.

【题目】“一带一路”国际合作高峰论坛圆满落幕了，相关话题在网络上引起了网友们的高度关注，为此，21财经APP联合UC推出“一带一路”大数据微报告，在全国抽取的70千万网民中(其中为高学历)有20千万人对此关注(其中为高学历).

(1)根据以上统计数据填下面列联表；

(2)根据列联表，用独立性检验的方法分析，能否有的把握认为“一带一路”的关注度与学历有关系？

	高学历(千万人)	不是高学历(千万人)	合计
关注
不关注
合计

参考公式：统计量的表达式是，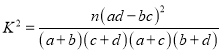

【题目】4月16日摩拜单车进驻大连市旅顺口区，绿色出行引领时尚，旅顺口区对市民进行“经常使用共享单车与年龄关系”的调查统计，若将单车用户按照年龄分为“年轻人”(20岁～39岁)和“非年轻人”(19岁及以下或者40岁及以上)两类，抽取一个容量为200的样本，将一周内使用的次数为6次或6次以上的称为“经常使用单车用户”。使用次数为5次或不足5次的称为“不常使用单车用户”，已知“经常使用单车用户”有120人，其中是“年轻人”，已知“不常使用单车用户”中有是“年轻人”.