题目内容
已知方程x3+ax2+bx+c=0的三个实根可分别作为一个椭圆、一双曲线、一抛物线的离心率.(1)求a+b+c的值;(2)求
的取值范围.
| b |
| a |
(1)令f(x)=x3+ax2+bx+c
∵抛物线的离心率为1
∴1是方程f(x)=x3+ax2+bx+c=0的一个实根
∴a+b+c=-1
(2)1+a+b+c=0得c=-1-a-b代入
f(x)=x3+ax2+bx-1-a-b
=(x-1)(x2+x+1)+a(x+1)(x-1)+b(x-1)=(x-1)[x2+(a+1)x+1+a+b]
设g(x)=x2+(a+1)x+1+a+b
g(x)=0的两根满足0<x1<1,x2>1
g(0)=1+a+b>0
g(1)=3+2a+b<0
用线性规划得-2<
<-
故答案为:-1,(-2,-
)
∵抛物线的离心率为1
∴1是方程f(x)=x3+ax2+bx+c=0的一个实根
∴a+b+c=-1
(2)1+a+b+c=0得c=-1-a-b代入
f(x)=x3+ax2+bx-1-a-b
=(x-1)(x2+x+1)+a(x+1)(x-1)+b(x-1)=(x-1)[x2+(a+1)x+1+a+b]
设g(x)=x2+(a+1)x+1+a+b
g(x)=0的两根满足0<x1<1,x2>1
g(0)=1+a+b>0
g(1)=3+2a+b<0
用线性规划得-2<
| b |
| a |
| 1 |
| 2 |
故答案为:-1,(-2,-
| 1 |
| 2 |

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
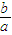 的取值范围.
的取值范围.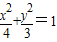 、一等轴双曲线、一抛物线的离心率,那么
、一等轴双曲线、一抛物线的离心率,那么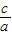 的值是 .
的值是 .