题目内容
已知方程x3+ax2+bx+c=0的三个实数根可分别作为一个椭圆| x2 |
| 4 |
| y2 |
| 3 |
| c |
| a |
分析:先求的三个曲线的离心率是
,
,1由此求出a、b、c
| 1 |
| 2 |
| 2 |
解答:解:曲线的离心率分别求出
,
,1,代入方程得
解得a=-
-
,c=-
故答案为
=3
-4
| 1 |
| 2 |
| 2 |
|
解得a=-
| 3 |
| 2 |
| 2 |
| ||
| 2 |
故答案为
| c |
| a |
| 2 |
点评:本题题目比较新颖,将椭圆、双曲线、抛物线联系起来很好.

练习册系列答案
相关题目
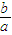 的取值范围.
的取值范围.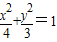 、一等轴双曲线、一抛物线的离心率,那么
、一等轴双曲线、一抛物线的离心率,那么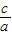 的值是 .
的值是 .