题目内容
已知方程x3+ax2+bx+c=0的三个实根可分别作为一个椭圆、一双曲线、一抛物线的离心率.(1)求a+b+c的值;(2)求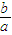 的取值范围.
的取值范围.
【答案】分析:(1)令f(x)=x3+ax2+bx+c,把x=1,y=0代入函数解析式求得a+b+c的值;
(2)然后求得a,b和c的关系代入函数解析式消去c,整理成f(x)=(x-1)(x2+x+1)+a(x+1)(x-1)+b(x-1)的形式,设g(x)=x2+(a+1)x+1+a+b椭圆和双曲线的离心率的范围确定两根的范围确定g(0)>0,g(1)<0,最后利用线性规划求得 的范围.
的范围.
解答:解:(1)令f(x)=x3+ax2+bx+c
∵抛物线的离心率为1
∴1是方程f(x)=x3+ax2+bx+c=0的一个实根
∴a+b+c=-1
(2)1+a+b+c=0得c=-1-a-b代入
f(x)=x3+ax2+bx-1-a-b
=(x-1)(x2+x+1)+a(x+1)(x-1)+b(x-1)=(x-1)[x2+(a+1)x+1+a+b]
设g(x)=x2+(a+1)x+1+a+b
g(x)=0的两根满足0<x1<1,x2>1
g(0)=1+a+b>0
g(1)=3+2a+b<0
用线性规划得-2< <-
<-
故答案为:-1,
点评:本题主要考查了函数的零点和根的分布,圆锥曲线的共同特征,线性规划的基础知识.考查基础知识的综合运用.
(2)然后求得a,b和c的关系代入函数解析式消去c,整理成f(x)=(x-1)(x2+x+1)+a(x+1)(x-1)+b(x-1)的形式,设g(x)=x2+(a+1)x+1+a+b椭圆和双曲线的离心率的范围确定两根的范围确定g(0)>0,g(1)<0,最后利用线性规划求得
 的范围.
的范围.解答:解:(1)令f(x)=x3+ax2+bx+c
∵抛物线的离心率为1
∴1是方程f(x)=x3+ax2+bx+c=0的一个实根
∴a+b+c=-1
(2)1+a+b+c=0得c=-1-a-b代入
f(x)=x3+ax2+bx-1-a-b
=(x-1)(x2+x+1)+a(x+1)(x-1)+b(x-1)=(x-1)[x2+(a+1)x+1+a+b]
设g(x)=x2+(a+1)x+1+a+b
g(x)=0的两根满足0<x1<1,x2>1
g(0)=1+a+b>0
g(1)=3+2a+b<0
用线性规划得-2<
 <-
<-
故答案为:-1,

点评:本题主要考查了函数的零点和根的分布,圆锥曲线的共同特征,线性规划的基础知识.考查基础知识的综合运用.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
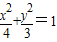 、一等轴双曲线、一抛物线的离心率,那么
、一等轴双曲线、一抛物线的离心率,那么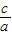 的值是 .
的值是 .